题目内容
12．
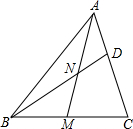如图所示，在△ABC中，AM是中线，N是AM的中点，BN的延长线交AC于点D，若AC=12，求CD的长．
分析 过M作ME∥BD交AC于E，根据ME∥BD，M为BC中点，N为AM中点推出AD=DE，CE=DE，求出AD=DE=CE=$\frac{1}{3}$AC，代入求出即可．
解答 解：
过M作ME∥BD交AC于E，
∵ME∥BD，M为BC中点，N为AM中点，
∴AD=DE，CE=DE，
∴AD=DE=CE=$\frac{1}{3}$AC，
∵AC=12，
∴AD=3．
点评 本题考查了三角形的中位线的性质的应用，能根据三角形的中位线定理求出AD=DE=CE是解此题的关键，注意：三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
2．
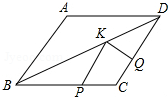如图，在菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）
如图，在菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）| A． | 2 | B． | 2$\sqrt{3}$ | C． | 4 | D． | 2$\sqrt{3}$+2 |
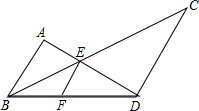如图，AB∥EF∥CD，E为AD与BC的交点，F在BD上，求证：$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$．
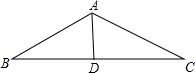如图，在△ABC中，AB=17，BC=30，BC边上的中线AD=8，∠B与∠C相等吗？
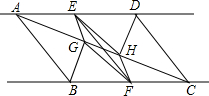如图，已知直线m∥n，A，D两点在直线m上，B，C两点在直线n上，且AB∥CD，E，F分别是AD，BC的中点，BG⊥AC，DH⊥AC，点G，H分别是垂足．求证：EF与GH互相平分．