题目内容
1．在一张纸上复制四个全等的直角三角形，通过拼图的方法验证勾股定理．你有哪些方法？并说说你的方法与课堂上的方法之间有什么联系与差别．分析 如图，根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积，代入数值，即可证明．
解答 
解：图（1）中的大正方形的面积可以表示为c2，也可表示为（b-a）2+4×$\frac{1}{2}$ab
∴（b-a）2+4×$\frac{1}{2}$ab=c2
化简得b2-2ab+b2+2ab=c2
∴当∠C=90°时，a2+b2=c2；
点评 本题考查利用图形面积的关系证明勾股定理，解题关键是利用三角形和正方形边长的关系进行组合图形．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
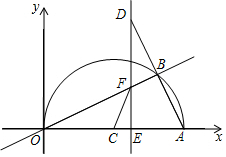如图，在平面直角坐标系中，点A（20，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．
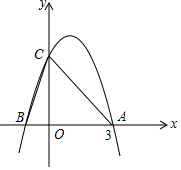如图所示，二次函数y=-x2+2x+m的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．
17．
如图，已知正方形ABCD的边长为5，点E、F分别在BC和CD边上，分别连接AE、AF、EF，若∠EAF=45°，则△CEF的周长是（ ）
如图，已知正方形ABCD的边长为5，点E、F分别在BC和CD边上，分别连接AE、AF、EF，若∠EAF=45°，则△CEF的周长是（ ）| A． | 6+2$\sqrt{3}$ | B． | 8.5 | C． | 10 | D． | 12 |