题目内容
17. 如图,已知正方形ABCD的边长为5,点E、F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )
如图,已知正方形ABCD的边长为5,点E、F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )| A. | 6+2$\sqrt{3}$ | B. | 8.5 | C. | 10 | D. | 12 |
分析 将△ABE绕点A逆时针旋转90°得到△ADH,根据旋转的性质可得HD=BE,AH=AE,∠DAH=∠BAE,然后求出∠FAH=∠EAF,再利用“边角边”证明△AEF和△AHF全等,根据全等三角形对应边相等可得EF=FH,然后求出△CEF的周长=BC+CD,再根据正方形的边长求解即可.
解答 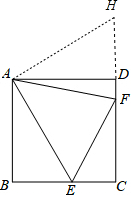 解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
由旋转的性质得,HD=BE,AH=AE,∠DAH=∠BAE,
所以,∠FAH=∠DAH+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-∠EAF,
∵∠EAF=45°,
∴∠FAH=90°-45°=45°,
∴∠FAH=∠EAF,
在△AEF和△AHF中,
$\left\{\begin{array}{l}{AH=AE}\\{∠FAH=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AHF(SAS),
∴EF=FH,
∴△CEF的周长=EF+CF+CE,
=FH+CF+CE,
=FD+DH+CF+CE,
=DF+BE+CF+CE,
=(BE+CE)+(DF+CF),
=BC+CD,
∵正方形ABCD的边长为5,
∴△CEF的周长为5+5=10.
故选C.
点评 本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,难点在于利用旋转变换作出全等三角形并用正方形的边长表示出△CEF的周长.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
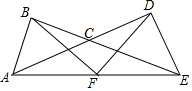 如图,两个等腰直角三角形ABC、CDE,顶点C重合,点B、C、E共线,F是AE的中点,连BF、DF,求证:BF=DF且BF⊥DF.
如图,两个等腰直角三角形ABC、CDE,顶点C重合,点B、C、E共线,F是AE的中点,连BF、DF,求证:BF=DF且BF⊥DF.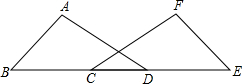 如图,在△ABD和△FEC中,点B、C、D、E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:AD=FC.
如图,在△ABD和△FEC中,点B、C、D、E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:AD=FC. 如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )
如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )