��Ŀ����
11��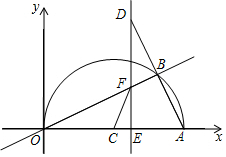 ��ͼ����ƽ��ֱ������ϵ�У���A��20��0������OAΪֱ���ڵ�һ����������ԲC����B�Ǹð�Բ����һ���㣬����OB��AB�����ӳ�AB����D��ʹDB=AB������D��x�ᴹ�ߣ��ֱ�x�ᡢֱ��OB�ڵ�E��F����EΪ���㣬����CF��
��ͼ����ƽ��ֱ������ϵ�У���A��20��0������OAΪֱ���ڵ�һ����������ԲC����B�Ǹð�Բ����һ���㣬����OB��AB�����ӳ�AB����D��ʹDB=AB������D��x�ᴹ�ߣ��ֱ�x�ᡢֱ��OB�ڵ�E��F����EΪ���㣬����CF����1������AOB=30��ʱ����OB�ij��ȣ�
��2����DE=16ʱ�����߶�EF�ij���
��3���ڵ�B�˶������У��Ƿ�����Ե�E��C��FΪ��������������AOB���ƣ������ڣ��������ʱ��E�����ꣻ�������ڣ���˵�����ɣ�
���� ��1������BC������֪�á�ACB=2��AOB=60�㣬AC=$\frac{1}{2}$AO=5�����ݻ�����ʽ��⣻
��2������OD���ɴ�ֱƽ���ߵ����ʵ�OD=OA=10����DE=8����Rt��ODE�У��ɹ��ɶ�����OE��������֤����OEF�ס�DEA���������Ʊ���EF���Ӷ������F�����꣬���ô���ϵ����������κ����Ľ���ʽ�����ɽ��
��3�����ڣ����Ե�E��C��FΪ��������������AOB����ʱ����Ϊ�ٵ�����E��O��C֮��ʱ�����Ե�E��C��FΪ��������������AOB���ƣ��С�ECF=��BOA���ECF=��OAB���ڵ�����E�ڵ�C���Ҳ�ʱ��Ҫʹ��ECF���BAO���ƣ�ֻ��ʹ��ECF=��BAO��
��� �⣺��1����ͼ1������BC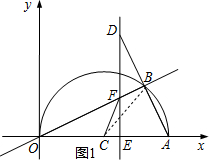
��A��10��0����
��OA=10��CA=5��
�ߡ�AOB=30�㣬
���ACB=2��AOB=60�㣬
�AB�ij�=$\frac{60•��•5}{180}$=$\frac{5��}{3}$��
��2������D�ڵ�һ���ޣ�
��ͼ2������OD��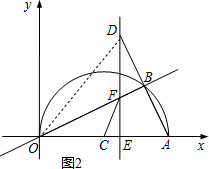
��OA�ǡ�Cֱ��
���OBA=90�㣬
�֡�AB=BD��
��OB��AD�Ĵ�ֱƽ���ߣ�
��OD=OA=10��
��Rt��ODE��
OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6��
��AE=AO-OE=10-6=4��
�ɡ�AOB=��ADE=90��-��OAB����OEF=��DEA��
�á�OEF�ס�DEA��
��$\frac{AE}{DE}$=$\frac{EF}{OE}$���� $\frac{4}{8}$=$\frac{EF}{6}$��
��EF=3��
���F��������6��4����
�����O��A��F�������ߵĽ���ʽΪy=ax2+bx+c��
�ѵ�O��0��0����A��10��0����F��6��4������y=ax2+bx+c��
�ã�$\left\{\begin{array}{l}{c=0}\\{100a+10b+c=0}\\{36a+6b+c=4}\end{array}\right.$��ã�$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{5}{3}}\\{c=0}\end{array}\right.$��
��y=-$\frac{1}{6}$x2+$\frac{5}{3}$x
����D�ڵڶ����ޣ�
��ͼ3������OD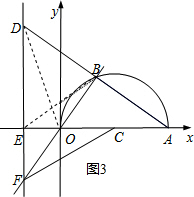
��OA�ǡ�Cֱ����
���OBA=90�㣬
�֡�AB=BD��
��OB��AD�Ĵ�ֱƽ���ߣ�
��OD=OA=10��
��Rt��ODE��
OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6��
��AE=AO+OE=10+6=16��
�ɡ�AOB=��ADE=90��-��OAB����OEF=��DEA��
�á�OEF�ס�DEA��
��$\frac{AE}{DE}$=$\frac{EF}{OE}$����=$\frac{16}{8}$=$\frac{EF}{6}$��
��EF=12��
���F��������-6��-12����
�����O��A��F�������ߵĽ���ʽΪy=ax2+bx+c��
�ѵ�O��0��0����A��10��0����F��-6��-12������õ���$\left\{\begin{array}{l}{c=0}\\{100a+10b+c=0}\\{36a-6b+c=-12}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{1}{8}}\\{b=\frac{5}{4}}\\{c=0}\end{array}\right.$��
��y=-$\frac{1}{8}$x2+$\frac{5}{4}$x��
��3����OE=x��
����ͼ4��������E��O��C֮��ʱ�����Ե�E��C��FΪ��������������AOB���ƣ��С�ECF=��BOA���ECF=��OAB��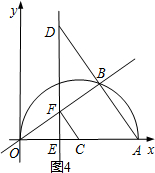
����ECF=��BOAʱ����ʱ��OCFΪ���������Σ���EΪOC
�е㣬��OE=$\frac{5}{2}$��
��E1�� $\frac{5}{2}$��0����
����ECF=��OABʱ����CE=5-x��AE=10-x��
��CF��AB����CF=$\frac{1}{2}$AB��
�ߡ�ECF�ס�EAD��
��$\frac{CE}{AE}$=$\frac{CF}{AD}$���� $\frac{5-x}{10-x}$=$\frac{1}{4}$����ã�x=$\frac{10}{3}$��
��E2�� $\frac{10}{3}$��0����
�ڵ�����E�ڵ�C���Ҳ�ʱ��
�ߡ�ECF����BOA��
��Ҫʹ��ECF���BAO���ƣ�ֻ��ʹ��ECF=��BAO
��ͼ5������BE��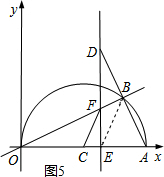
��BEΪRt��ADEб���ϵ����ߣ�
��BE=AB=BD��
���BEA=��BAO��
���BEA=��ECF��
��CF��BE��
��$\frac{CF}{BE}$=$\frac{OC}{OE}$��
�ߡ�ECF=��BAO����FEC=��DEA=90�㣬
���CEF�ס�AED��
��$\frac{CF}{AD}$=$\frac{CE}{AE}$��
��AD=2BE��
��$\frac{OC}{2OE}$=$\frac{CE}{AE}$��
�� $\frac{5}{2x}$=$\frac{x-5}{10-x}$��
��ã�x1=$\frac{5+5\sqrt{17}}{4}$��x2=$\frac{5-5\sqrt{17}}{4}$��0����ȥ����
��E3�� $\frac{5+5\sqrt{17}}{4}$��0����
��ʱ��E����Ϊ��E1�� $\frac{5}{2}$��0����E2�� $\frac{10}{3}$��0����E3�� $\frac{5+5\sqrt{17}}{4}$��0����
���� ���⿼��Բ�ۺ��⡢���������ε��ж������ʡ����ɶ��������á�Բ�ܽǶ�����������ʽ�����ã���������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�ѧ�����ò����������̽�����⣬�����п�ѹ���⣮

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�| A�� | Ϊ�˽���������ѧ����˯�������Ӧ�ò����ղ�ķ�ʽ | |
| B�� | ij�ֲ�Ʊ���н�������1%������100�����ֲ�Ʊһ�����н� | |
| C�� | һ������1��5��3��2��3��4��8����������λ������3 | |
| D�� | ���������ݵķ���s��2=0.1���������ݵķ���s��2=0.2�����������ݱȼ��������ȶ� |
| A�� | $\frac{1}{9}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
| A�� | 1 | B�� | $\frac{3}{2}$ | C�� | $\sqrt{5}$ | D�� | 3 |

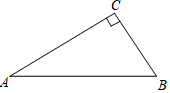 �۵���ͼ��ʾ��ֱ��������ֽƬABC��ʹ��C����AB�ϵĵ�E�����ۺ�ΪAD����D��BC���ϣ�����ֱ�ߺ�Բ�滭���ۺ�AD����������ͼ�ۼ�����д��������
�۵���ͼ��ʾ��ֱ��������ֽƬABC��ʹ��C����AB�ϵĵ�E�����ۺ�ΪAD����D��BC���ϣ�����ֱ�ߺ�Բ�滭���ۺ�AD����������ͼ�ۼ�����д��������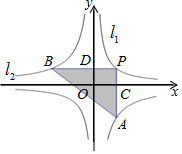 ��ͼ����������������$y=\frac{k}{x}$��y=-$\frac{2}{x}$��ͼ��ֱ���l1��l2��E��2��$\frac{1}{2}$����l1�ϵ�һ�㣮
��ͼ����������������$y=\frac{k}{x}$��y=-$\frac{2}{x}$��ͼ��ֱ���l1��l2��E��2��$\frac{1}{2}$����l1�ϵ�һ�㣮