题目内容
14.化简($\frac{1}{a-b}$-$\frac{1}{a+b}$)+$\frac{{ab}^{2}}{{a}^{2}{-b}^{2}}$,当a=$\sqrt{3}$-1,b=$\sqrt{3}$+1时,求出这个代数式的值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{a+b-a+b}{(a+b)(a-b)}$•$\frac{(a+b)(a-b)}{a{b}^{2}}$=$\frac{2b}{(a+b)(a-b)}$•$\frac{(a+b)(a-b)}{a{b}^{2}}$=$\frac{2}{ab}$,
故当a=$\sqrt{3}$+1,b=$\sqrt{3}$-1时,原式=$\frac{2}{ab}$=1.
点评 此题考查了分式的化简求值,以及根与系数的关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列各式的运算等于a6的是( )
| A. | a2•a3 | B. | a12÷a2 | C. | a3+a3 | D. | (a3)2 |
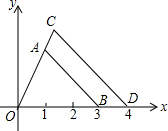 已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).
已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).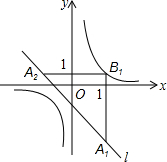 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013=-$\frac{1}{3}$.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013=-$\frac{1}{3}$.