题目内容
11. 如图,⊙O1与⊙O2外切于P点,过P的直线分别交两圆于A、B,AD切⊙O2于D,AD交⊙O1于C,己知PC=2,PB=8,求PD的长.
如图,⊙O1与⊙O2外切于P点,过P的直线分别交两圆于A、B,AD切⊙O2于D,AD交⊙O1于C,己知PC=2,PB=8,求PD的长.
分析 作⊙O1与⊙O2的公切线交AD于M,由弦切角定理得出∠MPC=∠A,∠MPD=∠B,∠CDP=∠B,得出∠CDP=∠MPD,由三角形的外角性质得出∠BPD=∠DPC,证出△BPD∽△DPC,得出对应边成比例,即可得出结果.
解答 解:作⊙O1与⊙O2的公切线交AD于M,如图所示:
则∠MPC=∠A,∠MPD=∠B,
∵AD切⊙O2于D,
∴∠CDP=∠B,
∴∠CDP=∠MPD,
∵∠BPD=∠A+∠CDP,
∴∠BPD=∠DPC,
∴△BPD∽△DPC,
∴PD:PC=PB:PD,
∴PD2=PC•PB=2×8=16,
∴PD=$\sqrt{16}$=4.
点评 本题中考查了相切两圆的切线性质、弦切角定理、相似三角形的判定与性质、三角形的外角性质等知识;熟练掌握相切两圆的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某冷饮店要根据去年同期的销售情况制定今年的销售计划,下面的调查数据中最值得关注的是( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
20. 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )| A. | 0 | B. | -2a | C. | -2b | D. | -2c |
1.下列计算中,不正确的是( )
| A. | 3$\sqrt{2}$×2$\sqrt{5}$=6$\sqrt{10}$ | B. | 3$\sqrt{6}$÷3$\sqrt{7}$=$\frac{6}{7}$ | C. | $\sqrt{2}$-5$\sqrt{2}$=-4$\sqrt{2}$ | D. | (3$\sqrt{2}$+2$\sqrt{3}$ )( 3$\sqrt{2}$-2$\sqrt{3}$)=6 |
 一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )
一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )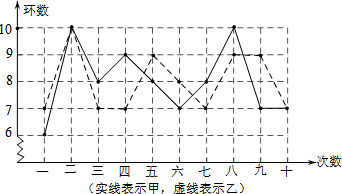
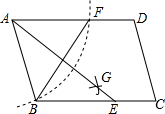 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )