题目内容
3.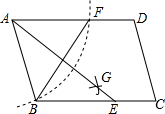 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,再根据平行四边形的性质得AF∥BE,得出∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图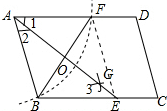
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AE=2AO=8.
故选C.
点评 本题考查了平行四边形的性质、勾股定理、平行线的性质、等腰三角形的判定;熟练掌握平行四边形的性质,由勾股定理求出AO是解决问题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
6.下列等式一定成立的是( )
| A. | 2m+3n=5mn | B. | (m3)2=m6 | C. | m2•m3=m6 | D. | (m-n)2=m2-n2 |
18.关于x的方程x2-4=0的根是( )
| A. | 2 | B. | -2 | C. | 2,-2 | D. | 2,$\frac{1}{2}$ |
8.化简2$\sqrt{8}$-$\sqrt{2}$-3$\sqrt{50}$-$\sqrt{12}$+$\sqrt{18}$的结果为( )
| A. | -$\sqrt{11}$ | B. | -9$\sqrt{2}$-2$\sqrt{3}$ | C. | -7$\sqrt{2}$ | D. | 2$\sqrt{3}$-9$\sqrt{2}$ |
 如图,⊙O1与⊙O2外切于P点,过P的直线分别交两圆于A、B,AD切⊙O2于D,AD交⊙O1于C,己知PC=2,PB=8,求PD的长.
如图,⊙O1与⊙O2外切于P点,过P的直线分别交两圆于A、B,AD切⊙O2于D,AD交⊙O1于C,己知PC=2,PB=8,求PD的长.