题目内容
2.观察与探究:
(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) |
| 正方形的个数 | 2 | 5 | 9 |
| 图形的周长 | 8 | 12 | 16 |
分析 (1)根据已知图形可以计算出图形(2)图形(3)的正方形个数、图形周长;
(2)观察(1)的规律,发现正方形个数可以利用等差数列加图形序号表示,而图形周长则可以通过图形四个方向线段和求解;
解答 解:(1)正方形个数可以根据图形得出;
图形的周长可以根据图形四个方向计算得出;
故答案为:5,9,12,16.
(2)通过观察发现以下规律:
图形1,正方形个数:1+1,
图形2,正方形个数:1+2+2,
图形3,正方形个数:1+2+3+3,
图形4,正方形个数:1+2+3+4+4,
∴根据以上规律:
图形n,正方形个数:1+2+3+4+5+…+n+n=$\frac{(1+n)n}{2}$=$\frac{{n}^{2}+n}{2}$;
通过观察图形从图形四个方向观察图形周长:
图形1,图形的周长:2+2+2+2,
图形2,图形的周长:3+3+3+3,
图形3,图形的周长:4+4+4+4,
图形4,图形的周长:5+5+5+5,
∴根据以上规律:
图形n,图形的周长:n+1+n+1+n+1+n+1=4n+4,
故答案为:$\frac{{n}^{2}+n}{2}$,4n+4.
点评 题目考查了图形的变化类,属于规律型题目求解,解决此类问题一定要找到图形序号与待求关系量之间的关系,另外掌握等差数列的求和公式对学生解决此类问题有很大帮助.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
1.函数y=-x2-3的图象向上平移2个单位,再向左平移2个单位后,得到的函数是( )
| A. | y=-(x+2)2-1 | B. | y=-(x-2)2-1 | C. | y=-(x-2)2+1 | D. | y=-(x+2)2+1 |
14. 如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
 如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )| A. | 20 | B. | 16 | C. | 25 | D. | 30 |
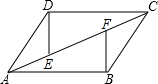 已知CD=AB,CD∥AB,AE=CF,求证:AD∥BC.
已知CD=AB,CD∥AB,AE=CF,求证:AD∥BC.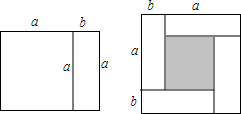
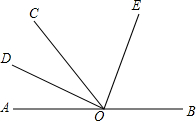 如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.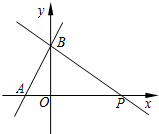 如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.
如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.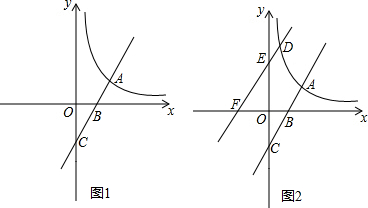
 如图,已知:CA⊥AB,DB⊥AB,AD与BC交于点E,∠CAD=∠DBC.求证:CA=DB.
如图,已知:CA⊥AB,DB⊥AB,AD与BC交于点E,∠CAD=∠DBC.求证:CA=DB.