题目内容
7.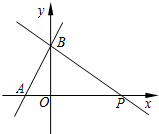 如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.
如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.(1)求m的值及点A的坐标;
(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=3OA,求直线BP的函数表达式.
分析 (1)先利于y=(m+1)x+$\frac{3}{2}$可求出B(0,$\frac{3}{2}$),所以OB=$\frac{3}{2}$,则利用三角形面积公式计算出OA=1,则A(-1,0);然后把点A(-1,0)代入y=(m+1)x+$\frac{3}{2}$可求出m的值;
(2)利用OP=3OA=3可得到点P的坐标为(3,0),然后利用待定系数法求直线BP的函数解析式.
解答 解:(1)当x=0时,y=(m+1)x+$\frac{3}{2}$=$\frac{3}{2}$,则B(0,$\frac{3}{2}$),所以OB=$\frac{3}{2}$,
∵S△OAB=$\frac{3}{4}$,
∴$\frac{1}{2}$×OA×OB=$\frac{3}{4}$,解得OA=1,
∴A(-1,0);
把点A(-1,0)代入y=(m+1)x+$\frac{3}{2}$得-m-1+$\frac{3}{2}$=0,
∴m=$\frac{1}{2}$;
(2)∵OP=3OA,
∴OP=3,
∴点P的坐标为(3,0),
设直线BP的函数表达式为y=kx+b,
把P(3,0)、B(0,$\frac{3}{2}$)代入得$\left\{\begin{array}{l}{3k+b=0}\\{b=\frac{3}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线BP的函数表达式为y=-$\frac{1}{2}$x+$\frac{3}{2}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.


(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) |
| 正方形的个数 | 2 | 5 | 9 |
| 图形的周长 | 8 | 12 | 16 |
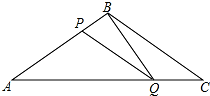 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒. 如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.
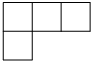
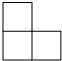
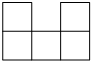
如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.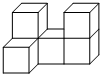 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )
如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )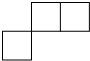
 如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD. 如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )