题目内容
12. 如图,已知:CA⊥AB,DB⊥AB,AD与BC交于点E,∠CAD=∠DBC.求证:CA=DB.
如图,已知:CA⊥AB,DB⊥AB,AD与BC交于点E,∠CAD=∠DBC.求证:CA=DB.
分析 先根据垂直定义得到∠CAB=∠DBA=90°,再利用等角的余角相等得到∠DAB=∠CBA,于是可根据“ASA”判断△CAB≌△DBA,然后根据全等三角形的性质得CA=DB.
解答 证明: 如图,
如图,
∵CA⊥AB,DB⊥AB,
∴∠CAB=∠DBA=90°,
∵∠CAD=∠DBC,
∴∠CAB-∠CAD=∠DBA-∠DBC,即∠DAB=∠CBA,
在△CAB和△DBA中,
$\left\{\begin{array}{l}{∠CAB=∠DBA}\\{AB=BA}\\{∠CAB=∠DAB}\end{array}\right.$,
∴△CAB≌△DBA,
∴CA=DB.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形;在应用全等三角形的性质时主要是得到对应角相等或对应线段相等.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.观察与探究:

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为$\frac{{n}^{2}+n}{2}$,周长为4n+4.

(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) |
| 正方形的个数 | 2 | 5 | 9 |
| 图形的周长 | 8 | 12 | 16 |
3.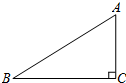 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )| A. | $\frac{{\sqrt{7}}}{3}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
20.下列图案中,是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (-3,-2) |
1.下列各数中,最小的数是( )
| A. | 2 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB.
如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB. 如图所示:点B,C在线段AD上,点B为AC的中点,若BC=4cm,AD=15cm,那么BD=11cm.
如图所示:点B,C在线段AD上,点B为AC的中点,若BC=4cm,AD=15cm,那么BD=11cm.