题目内容
1.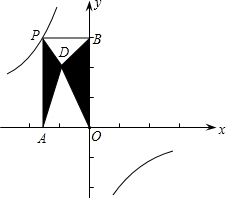 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )| A. | y=-$\frac{5}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{10}{x}$ | D. | y=-$\frac{12}{x}$ |
分析 根据反比例函数的几何意义,以及S阴影=$\frac{1}{2}$S矩形OAPB即可求解.
解答 解:∵S阴影=$\frac{1}{2}$S矩形OAPB=$\frac{1}{2}$|k|=-$\frac{1}{2}$k=5,
解得:k=-10.
则反比例函数的解析式是y=-$\frac{10}{x}$.
故选C.
点评 本题主要考查反比例函数系数k的几何意义,反比例函数$y=\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
相关题目
11. 如图,在⊙O中,∠BAC=33°,则∠BOC的度数是( )
如图,在⊙O中,∠BAC=33°,则∠BOC的度数是( )
 如图,在⊙O中,∠BAC=33°,则∠BOC的度数是( )
如图,在⊙O中,∠BAC=33°,则∠BOC的度数是( )| A. | 33° | B. | 66° | C. | 60° | D. | 45° |
9. 如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
 如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )| A. | 72° | B. | 54° | C. | 46° | D. | 115° |
16.下列说法不正确的是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 有一组邻边相等、一个角是直角的四边形是正方形 |
6. 利用如图的两个转盘进行“配紫色”的游戏,能配得紫色的概率是( )
利用如图的两个转盘进行“配紫色”的游戏,能配得紫色的概率是( )
 利用如图的两个转盘进行“配紫色”的游戏,能配得紫色的概率是( )
利用如图的两个转盘进行“配紫色”的游戏,能配得紫色的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$. |
 如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
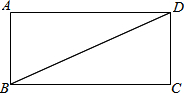 (1)在图中作出△CDB沿对角线BD所在的直线对折后的△C1DB,C点的对应点为C1(用尺规作图,保留清晰的作图痕迹,不写作法);
(1)在图中作出△CDB沿对角线BD所在的直线对折后的△C1DB,C点的对应点为C1(用尺规作图,保留清晰的作图痕迹,不写作法);