题目内容
8. AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.
AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.
分析 根据圆周角定理得∠ACB=90°,∠A=∠D=30°,然后在Rt△ACB中,利用∠A的正切可计算出AC的长.
解答 解:∵AB为直径,
∴∠ACB=90°,
∵∠A=∠D=30°,
在Rt△ACB中,∵tan∠A=$\frac{BC}{AC}$,
∴AC=$\frac{3}{tan30°}$=3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.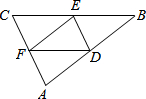 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )
 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )| A. | 8cm | B. | 6cm | C. | 5cm | D. | 4cm |
19.若(m-1)x>m-1的解集为x<1,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m>0 | D. | m<0 |
16.下列说法不正确的是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 有一组邻边相等、一个角是直角的四边形是正方形 |
3.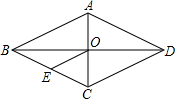 已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
 如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.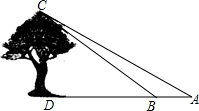 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71) 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.