题目内容
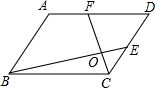如图，平行四边形ABCD中，F为AD中点，CO=| 1 |
| 2 |
考点：平行四边形的性质,平行线分线段成比例
专题：
分析：延长BA、CF相交于点G，根据平行线分线段成比例定理可得AB=AG，CF=FG，然后求出
，再根据平行线分线段成比例定理可得
=
，然后求解即可．
| CO |
| OG |
| CE |
| BG |
| CO |
| OG |
解答：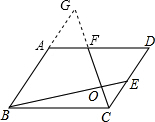
解：如图，延长BA、CF相交于点G，
∵点F是AD的中点，
∴AF=DF=
BC，
∵AD∥BC，
∴
=
=
=
，
∴AB=AG，CF=FG，
∵CO=
FO，
∴
=
=
，
∴
=
=
，
∵BG=AB+AG=2AB，
∴
=
，
即CE：AB=2：5．
故答案为：2：5．
解：如图，延长BA、CF相交于点G，∵点F是AD的中点，
∴AF=DF=
| 1 |
| 2 |
∵AD∥BC，
∴
| AG |
| BG |
| GF |
| CG |
| AF |
| BC |
| 1 |
| 2 |
∴AB=AG，CF=FG，
∵CO=
| 1 |
| 2 |
∴
| CO |
| OG |
| 1 |
| (1+2)+2 |
| 1 |
| 5 |
∴
| CE |
| BG |
| CO |
| OG |
| 1 |
| 5 |
∵BG=AB+AG=2AB，
∴
| CE |
| AB |
| 2 |
| 5 |
即CE：AB=2：5．
故答案为：2：5．
点评：本题考查了平行四边形的性质，平行线分线段成比例定理，熟记性质与定理并作辅助线是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
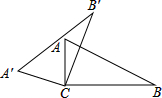如图，将Rt△ABC绕C点逆时针旋转得到△A′B′C′，若∠A′BC=160°，则此图形旋转角是
从△ABC的顶点A引三条线段：∠A的平分线AM，∠A的外角平分线AN，三角形外接圆的切线AK，点M、K、N依次排列在直线BC上，证明：MK=KN．
我们把两相邻边分别相等的四边形叫做“筝形”．如图，在筝形ABCD中，AB=AD，BC=DC，AC、BD相交于点O．
已知在△ABC中，D是AB上一点，P是AC上一点．从14点到14点20分，钟表的分针转过的角度是（ ）
| A、10° | B、60° |
| C、90° | D、120° |