题目内容
11.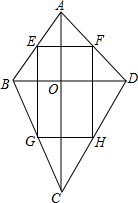 如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,
如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,(1)试确定四边形EGHF的形状,并说明理由;
(2)若四边形EGHF的面积为4,求四边形ABCD的面积.
分析 (1)根据三角形中位线定理得到EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,得到EF=GH,EF∥GH,根据平行四边形的判定定理得到四边形EGHF是平行四边形,证明EG⊥EF,得到四边形EGHF为矩形;
(2)根据菱形的面积等于对角线乘积的一半计算即可.
解答 解:(1)四边形EGHF为矩形,
∵E、F是AB、AD的中点,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∵G、H是BC、DC的中点,
∴GH∥BD,GH=$\frac{1}{2}$BD,
∴EF=GH,EF∥GH,
∴四边形EGHF是平行四边形,
∵EF∥BD,AC⊥BD,
∴AC⊥EF,
∵E、G是AB、BC的中点,
∴EG∥AC,EG=$\frac{1}{2}$AC,
∴EG⊥EF,
∴四边形EGHF为矩形;
(2)∵EF=$\frac{1}{2}$BD,EG=$\frac{1}{2}$AC,
∴$\frac{1}{4}$BD×AC=4,
则$\frac{1}{2}$BD×AC=8,
∴四边形ABCD的面积为8.
点评 本题考查的是三角形中位线定理、矩形的判定和菱形的面积计算,掌握三角形中位线平行于第三边并且等于第三边的一半是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
1.下列计算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}÷\sqrt{2}$=4 | C. | $\sqrt{27}$=3$\sqrt{3}$ | D. | (1+$\sqrt{2})(1-\sqrt{2})=1$(1-$\sqrt{2}$)=1 |
20.某商人在一次买卖中均以168元卖出两套服装,其中一套盈利20%,另一套亏本20%,该商贩在这次经营中( )
| A. | 亏本14元 | B. | 盈利14元 | C. | 不亏不盈 | D. | 盈利20元 |
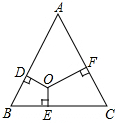 如图,等边三角形ABC的边长为4,高为h.
如图,等边三角形ABC的边长为4,高为h.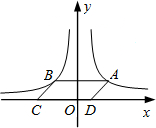 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7.
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7. 如图,AB、CD相交于点O,∠C=∠COA,∠D=∠BOD,试说明AC∥BD.
如图,AB、CD相交于点O,∠C=∠COA,∠D=∠BOD,试说明AC∥BD. 已知如图,OP平分∠AOB,PE⊥AO,PF⊥BO,垂足分别为E、F.
已知如图,OP平分∠AOB,PE⊥AO,PF⊥BO,垂足分别为E、F.