题目内容
1. 已知如图,OP平分∠AOB,PE⊥AO,PF⊥BO,垂足分别为E、F.
已知如图,OP平分∠AOB,PE⊥AO,PF⊥BO,垂足分别为E、F.(1)求证:PE=PF.
(2)将∠EPF绕点P进行旋转,角的两边与OA、OB分别交于E、F两点,问(1)中的结论是否仍然成立.并说明理由.
分析 (1)根据角平分线的性质即可得到结论;
(2)如图,过点P作PM⊥OA,PN⊥OB,垂足是M,N,则∠PME=∠PNF=90°,由OP平分∠AOB,得到PM=PN,证得∠MPE=∠FPN,推出△PEM≌△PFN(ASA),即可得到结论.
解答 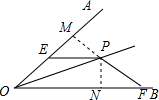 (1)证明:∵OP平分∠AOB,PE⊥AO,PF⊥BO,
(1)证明:∵OP平分∠AOB,PE⊥AO,PF⊥BO,
∴PE=PF;
(2)成立,
理由是:如图,过点P作PM⊥OA,PN⊥OB,垂足是M,N,
则∠PME=∠PNF=90°,
∵OP平分∠AOB,
∴PM=PN,
∵∠AOB=∠PME=∠PNF=90°,
∴∠MPN=90°,
∵∠EPF=90°,
∴∠MPE=∠FPN,
在△PEM和△PFN中,$\left\{\begin{array}{l}{∠PME=∠PNF}\\{PM=PN}\\{∠MPE=∠NPF}\end{array}\right.$,
∴△PEM≌△PFN(ASA),
∴PE=PF.
点评 本题主要考查了角平分线的性质,全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,

练习册系列答案
相关题目
16.任意三角形两边中点的连线与第三边上的中线( )
| A. | 互相平分 | B. | 互相垂直 | C. | 相等 | D. | 互相垂直平分 |
6.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
那么,当输入数据是8时,输出的数据是( )
| 输入 | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | $\frac{1}{2}$ | $\frac{2}{7}$ | $\frac{3}{14}$ | $\frac{4}{23}$ | $\frac{5}{34}$ | … |
| A. | $\frac{8}{78}$ | B. | $\frac{8}{79}$ | C. | $\frac{8}{80}$ | D. | $\frac{8}{81}$ |
13.直角三角形两条边的长分别为:3,4,则第三边的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 7 | D. | 5或$\sqrt{7}$ |
10.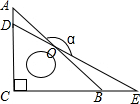 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )| A. | 165° | B. | 135° | C. | 115° | D. | 95° |
11.下列图形中既是中心对称又是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 角 | D. | 菱形 |
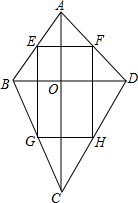 如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,
如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,