Question

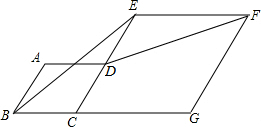如图，菱形ABCD的边CD在菱形ECGF的边CE上，且D是CE中点．连接BE，DF．
（1）观察猜想BE与DF之间的大小关系，并证明你的结论．
（2）图中是否存在旋转能够互相重合的两个三角形？若存在，请说明旋转过程；若不存在，请说明理由．

Answer 1

考点：菱形的性质,全等三角形的判定与性质,旋转的性质

专题：

分析：（1）根据两直线平行，内错角相等可得∠BCE=∠DEF，再根据线段中点的定义可得CD=DE，菱形的邻边相等可得BC=CD，CE=EF，从而得到BC=DE，然后利用“边角边”证明△BCE和△DEF全等，根据全等三角形对应边相等可得BE=DF；
（2）设AD、BE相交于点H，根据旋转的性质，△ABH和△DEH旋转后能够互相重合．

解答：解：（1）∵菱形CEFG的对边CG∥EF，
∴∠BCE=∠DEF，
∵D是CE中点，
∴CD=DE，
在菱形ABCD和菱形ECGF中，BC=CD，CE=EF，
∴BC=DE，
在△BCE和△DEF中，

BC=DE ∠BCE=∠DEF CE=EF

，
∴△BCE≌△DEF（SAS），
∴BE=DF；

（2）如图，设AD、BE相交于点H，
△ABH绕点H旋转180°后能够与△DEH互相重合．

点评：本题考查了菱形的性质，全等三角形的判定与性质，旋转的性质，熟记各性质并是解题的关键，（2）难点在于准确识图．