题目内容
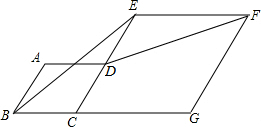
已知：如图，B、F、C、D在同一条直线上，∠ACB=∠EFD，BF=CD，AC=EF．求证：AB∥ED．考点：全等三角形的判定与性质
专题：证明题
分析：先根据BF=CD得出BC=DF，再由SAS定理得出△ABC≌△EDF，由全等三角形的性质得出∠B=∠D，由此可得出结论．
解答：证明：∵BF=CD，
∴BF+FC=CD+FC，即BC=DF．
在△ABC与△EDF中，
，
∴△ABC≌△EDF（SAS），
∴∠B=∠D，
∴AB∥ED．
∴BF+FC=CD+FC，即BC=DF．
在△ABC与△EDF中，
|
∴△ABC≌△EDF（SAS），
∴∠B=∠D，
∴AB∥ED．
点评：本题考查的是全等三角形的判定与性质，熟知SAS定理是解答此题的关键．
练习册系列答案
相关题目
已知以下三个数，不能组成直角三角形的是（ ）
| A、9、12、15 | ||||
B、
| ||||
| C、0.3、0.4、0.5 | ||||
| D、32、42、52 |
某同学一家三口随旅游团去九寨沟旅游，该同学把旅途费用支出情况制成了如图的统计图：
已知，如图，在△ABC中，AD，AE分别是△ABC的高和角平分线，
如图，菱形ABCD的边CD在菱形ECGF的边CE上，且D是CE中点．连接BE，DF．