题目内容
某零件制造车间有20名工人,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利150元,每制造一个乙种零件可获利260元.在这20名工人中.
(1)如何安排工人使得每天所获利润为22000元?
(2)若要使每天所获利润不低于24000元,至少要派多少名工人去制造乙种零件?
(1)如何安排工人使得每天所获利润为22000元?
(2)若要使每天所获利润不低于24000元,至少要派多少名工人去制造乙种零件?
考点:一元一次不等式的应用,二元一次方程组的应用
专题:
分析:(1)根据每天所获利润=甲种零件所获利润+乙种零件所获利润,可列出关系式求出即可;
(2)根据车间每天所获利润不低于24000元,可列出不等式.
(2)根据车间每天所获利润不低于24000元,可列出不等式.
解答:解:(1)设安排x人制造甲种零件,则安排(20-x)制造乙种零件,根据题意,可得:
22000=150×6x+260×5(20-x)
即22000=-400x+26000,
解得:x=10,
故20-x=10.
答:安排10人制造甲种零件,10人制造乙种零件;
(2)由题意,-400x+26000≥24000,
令-400x+26000=24000,
解得x=5.因为y=-400x+26000中,
∵-400<0,
∴y的值随x的值的增大而减少,
∴要使-400x+26000≥24000,需x≤5,
即最多可派5名工人制造甲种零件,
此时有20-x=20-5=15(名).
答:至少要派15名工人制造乙种零件才合适.
22000=150×6x+260×5(20-x)
即22000=-400x+26000,
解得:x=10,
故20-x=10.
答:安排10人制造甲种零件,10人制造乙种零件;
(2)由题意,-400x+26000≥24000,
令-400x+26000=24000,
解得x=5.因为y=-400x+26000中,
∵-400<0,
∴y的值随x的值的增大而减少,
∴要使-400x+26000≥24000,需x≤5,
即最多可派5名工人制造甲种零件,
此时有20-x=20-5=15(名).
答:至少要派15名工人制造乙种零件才合适.
点评:本题主要考查了一元一次方程的应用以及一元一次不等式的应用,正确得出找出各个量之间的关系式,列出关系式或不等式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,
已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,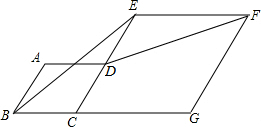 如图,菱形ABCD的边CD在菱形ECGF的边CE上,且D是CE中点.连接BE,DF.
如图,菱形ABCD的边CD在菱形ECGF的边CE上,且D是CE中点.连接BE,DF. 将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):