Question

6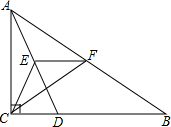．如图，在△ABC中，∠ACB=90°，点E，F分别是AD，AB中点，AD=BD
（1）求证：△CEF是等腰三角形；
（2）若AD=a，AB=b，求△CEF的周长．

Answer 1

分析 （1）根据三角形中位线定理得到EF=$\frac{1}{2}$BD，根据直角三角形的性质得到CE=$\frac{1}{2}$AD，根据题意得到CE=EF；
（2）根据三角形中位线定理、直角三角形的性质求出CE=EF=$\frac{1}{2}$a，CF=$\frac{1}{2}$b，根据周长公式计算即可．

解答 （1）证明：∵点E，F分别是AD，AB中点，
∴EF=$\frac{1}{2}$BD，
∵∠ACB=90°，点E是AD的中点，
∴CE=$\frac{1}{2}$AD，
∵AD=BD，
∴CE=EF，
∴△CEF是等腰三角形；
（2）解：由（1）得，CE=EF=$\frac{1}{2}$AD=$\frac{1}{2}$a，
∵∠ACB=90°，点F是AB中点，
∴CF=$\frac{1}{2}$AB=$\frac{1}{2}$b，
∴△CEF的周长=a+$\frac{1}{2}$b．

点评 本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边且等于第三边的一半、直角三角形斜边上的中线是斜边的一半是解题的关键．