题目内容
14.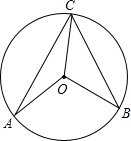 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
分析 延长CO交⊙O于点D,先根据圆周角定理求出∠BOD的度数,再由∠CAO=25°,CO=OA得出∠ACO=∠CAO=25°,由圆周角定理求出∠AOD的度数,进而可得出结论.
解答  解:延长CO交⊙O于点D,
解:延长CO交⊙O于点D,
∵∠BCO=35°,
∴∠BOD=70°.
∵∠CAO=25°,CO=OA,
∴∠ACO=∠CAO=25°,
∴∠AOD=2∠ACO=50°,
∴∠AOB=50°+70°=120°.
故选C.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
5.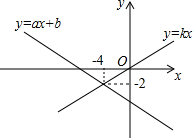 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
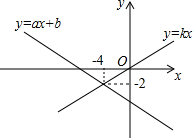 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )| A. | x>-4 | B. | x<-2 | C. | x<-4 | D. | x>-2 |
4.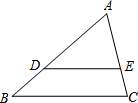 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:DB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:DB=( )| A. | 1:2 | B. | 4:9 | C. | 2:3 | D. | 2:1 |
 如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?
如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数? 一个木工做一个矩形的桌面,完工后,量得桌面的长为60厘米,宽为32厘米,对角线为68厘米,这个桌面是合格的吗?请说明理由.
一个木工做一个矩形的桌面,完工后,量得桌面的长为60厘米,宽为32厘米,对角线为68厘米,这个桌面是合格的吗?请说明理由.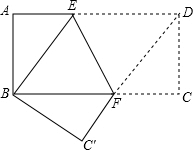 如图:矩形ABCD中,AB=8cm,AD=16cm,将矩形折叠,使点D与点B重合,折痕为EF.
如图:矩形ABCD中,AB=8cm,AD=16cm,将矩形折叠,使点D与点B重合,折痕为EF.