题目内容
16.从五个点(-2,6)、(-3,4)、(2,6)、(6,-2)、(4,-2)中任取一点,在双曲线y=$\frac{12}{x}$上的概率是$\frac{1}{5}$.分析 首先找出在双曲线y=$\frac{12}{x}$上点的个数,然后根据概率公式求出答案.
解答 解:∵五个点(-2,6)、(-3,4)、(2,6)、(6,-2)、(4,-2)中,在双曲线y=$\frac{12}{x}$上的点有(2,6)一共1个,
∴五点任取一点,在双曲线y=$\frac{12}{x}$上的概率是$\frac{1}{5}$,
故答案为$\frac{1}{5}$.
点评 本题主要考查概率公式的知识,解答本题关键是掌握概率=所求情况数与总情况数之比,此题难度不大.

练习册系列答案
相关题目
5.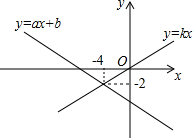 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
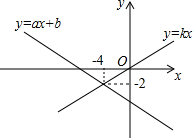 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )| A. | x>-4 | B. | x<-2 | C. | x<-4 | D. | x>-2 |
 如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?
如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数? 如图,在⊙O中,AB=AC,∠A=50°,求∠ABC的度数.
如图,在⊙O中,AB=AC,∠A=50°,求∠ABC的度数.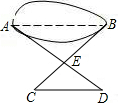 为了测量水塘边A、B两点之间的距离,在可以看到A、B的E处,取AE、BE延长线上的C、D两点,使CD∥AB.如果测量得CD=5米,AD=15米,ED=3米,你能求出AB两点之间的距离吗?
为了测量水塘边A、B两点之间的距离,在可以看到A、B的E处,取AE、BE延长线上的C、D两点,使CD∥AB.如果测量得CD=5米,AD=15米,ED=3米,你能求出AB两点之间的距离吗?