Question

16．如图所示，正方形ABCD是⊙O的内接四边形，△AEB是以AB为底的等腰三角形，且△AEB的面积为2（1+$\sqrt{2}$），求阴影部分的面积．

Answer 1

分析 连接OA，OB，在EF⊥AB于F，则EF过O，有等腰三角形的性质得到AF=BF，设⊙O的半径为R，由正方形ABCD是⊙O的内接四边形得到∠AOB=90°，根据勾股定理AB=$\sqrt{2}$R，OF=$\frac{\sqrt{2}}{2}$R，故有AF=R+$\frac{\sqrt{2}}{2}$R，根据已知条件可求得R，由阴影部分的面积=⊙O的面积-△AEB的面积代入数值即可求得结论．

解答 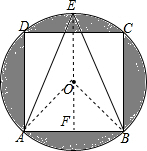解：连接OA，OB，在EF⊥AB于F，则EF过O，AF=BF，
设⊙O的半径为R，
∵正方形ABCD是⊙O的内接四边形，
∴∠AOB=90°，OA=OB=R，
∴AB=$\sqrt{2}$R，
∴OF=$\frac{\sqrt{2}}{2}$R，
∴AF=R+$\frac{\sqrt{2}}{2}$R，
∵△AEB的面积为=$\frac{1}{2}$AB•EF=2（1+$\sqrt{2}$），
∴2（1+$\sqrt{2}$）=$\frac{1}{2}$$\sqrt{2}$R（1+$\frac{\sqrt{2}}{2}$）R，
即R²=4，
∴R=2，
∴阴影部分的面积=⊙O的面积-△AEB的面积=4π-2（1+$\sqrt{2}$）．

点评 本题主要考查了等腰三角形的性质，正多边形和园，正确做出辅助线是解决问题的关键．