题目内容
20.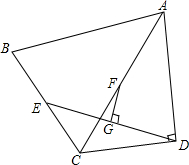 如图,在四边形ABCD中,∠ADC=90°,AC=AB,点E、F分别是BC、AC的中点,GF⊥DE,点G为垂足,求证:EG=DG.
如图,在四边形ABCD中,∠ADC=90°,AC=AB,点E、F分别是BC、AC的中点,GF⊥DE,点G为垂足,求证:EG=DG.
分析 连接AE,EF,DF,根据三角形中位线的性质得到EF=$\frac{1}{2}$AB,由直角三角形斜边上的中线等于斜边的一半得到DF=$\frac{1}{2}$AC,然后由等腰三角形的性质得到结论.
解答 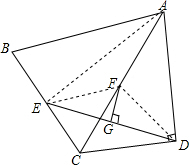 证明:连接AE,EF,DF,
证明:连接AE,EF,DF,
∵点E、F分别是BC、AC的中点,
∴EF=$\frac{1}{2}$AB,
∵AB=AC,
∴EF=$\frac{1}{2}$AC,
∵∠ADC=90°,
∴DF=$\frac{1}{2}$AC,
∴EF=DF,
∵GF⊥DE,
∴EG=DG.
点评 本题考查了直角三角形的性质,直角三角形斜边上的中线等于斜边的一半,还考查了等腰三角形的判定和性质,三角形的中位线定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
12.下列方程的解是x=2的是( )
| A. | x-$\frac{1}{2}$=0 | B. | 6x-12=0 | C. | -4x+6=0 | D. | 2x+4=0 |
8. 如图,在⊙O中,弦的条数是( )
如图,在⊙O中,弦的条数是( )
 如图,在⊙O中,弦的条数是( )
如图,在⊙O中,弦的条数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 以上均不正确 |
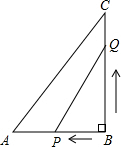 如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.
如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.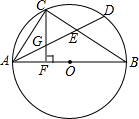 AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.
AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF. 如图,已知△ABC和点O,将△ABC绕点O旋转,点A的对应点为点D,画出△ABC经旋转后得到的图形.
如图,已知△ABC和点O,将△ABC绕点O旋转,点A的对应点为点D,画出△ABC经旋转后得到的图形. 如图,0A、0B都是⊙0的半径,∠A0B=100°,异于A、B的动点C在⊙0上,求∠ACB的度数.
如图,0A、0B都是⊙0的半径,∠A0B=100°,异于A、B的动点C在⊙0上,求∠ACB的度数.