题目内容
12.下列方程的解是x=2的是( )| A. | x-$\frac{1}{2}$=0 | B. | 6x-12=0 | C. | -4x+6=0 | D. | 2x+4=0 |
分析 使方程左右两边的值相等的未知数的值是该方程的解.检验一个数是否为相应的方程的解,就是把这个数代替方程中的未知数,看左右两边的值是否相等,如果左边=右边,那么这个数就是该方程的解;反之,这个数就不是该方程的解.
解答 解:A、当x=2时,左边=2-$\frac{1}{2}$=$\frac{3}{2}$,左边≠右边,故A错误;
B、当x=2时,左边=2×6-12=0,左边=右边,故B正确;
C、当x=2时,左边=-8+6=-2,左边≠右边,故C错误;
D、当x=2时,左边=4+4=8,左边≠右边,故C错误;
故选:B.
点评 本题考查了方程的解,解题的关键是根据方程的解的定义:使方程左右两边的值相等的未知数的值是该方程的解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17.下列运用等式的性质对等式进行的变形中,正确的是( )
| A. | 若x=y,则x-5=y+5 | B. | 若a=b,则ac=bc | ||
| C. | 若$\frac{a}{2c}$=$\frac{b}{3c}$则2a=3b | D. | 若x=y,则$\frac{x}{a}$=$\frac{y}{b}$ |
4.下列变形中不正确的是( )
| A. | 从2x-1=6,得到2x=6+1 | B. | 从-11x=6,得到x=-$\frac{11}{6}$ | ||
| C. | 从-$\frac{2}{3}$x=-$\frac{2}{3}$,得到x=1 | D. | 从$\frac{x}{2}$=0,得到x=0 |
 若双曲线y=$\frac{k}{x}$与边长为5的等边△A0B的边0A,AB分别相交于C,D两点,且DC垂直于AO,求实数k的值.
若双曲线y=$\frac{k}{x}$与边长为5的等边△A0B的边0A,AB分别相交于C,D两点,且DC垂直于AO,求实数k的值.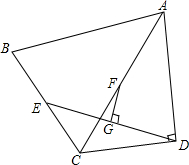 如图,在四边形ABCD中,∠ADC=90°,AC=AB,点E、F分别是BC、AC的中点,GF⊥DE,点G为垂足,求证:EG=DG.
如图,在四边形ABCD中,∠ADC=90°,AC=AB,点E、F分别是BC、AC的中点,GF⊥DE,点G为垂足,求证:EG=DG.