题目内容
18. 如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.(1)求证:GH=GF;
(2)试说明∠FGH与∠BAC互补.
分析 (1)首先得出△ABD≌△ACE(SAS),进而利用三角形中位线定理得出GH=GF;
(2)利用全等三角形的性质结合平行线的性质得出∠FGH=∠DGF+∠HGD进而得出答案.
解答 证明:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵F,G,H分别为BC,CD,DE的中点,
∴HG∥CE,GF∥BD,且GH=$\frac{1}{2}$CE,GF=$\frac{1}{2}$BD,
∴GH=GF;
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵HG∥CE,GF∥BD,
∴∠HGD=∠ECD,∠GFC=∠DBC,
∴∠HGD=∠ACD+∠ECA=∠ACD+∠ABD,
∠DGF=∠GFC+∠GCF=∠DBC+∠GCF,
∴∠FGH=∠DGF+∠HGD
=∠DBC+∠GCF+∠ACD+∠ABD
=∠ABC+∠ACB
=180°-∠BAC,
∴∠FGH与∠BAC互补.
点评 此题主要考查了全等三角形的判定与性质以及三角形中位线定理,正确得出△ABD≌△ACE是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
特别说明:毛利润=售价-进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是5元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为y元.
①当y=1080时,求m的值;
②朝阳灯饰商场把购进的这两种型号节能灯全部销售完时,所获得的毛利润最多是1400元.(请直接写出答案)
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是5元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为y元.
①当y=1080时,求m的值;
②朝阳灯饰商场把购进的这两种型号节能灯全部销售完时,所获得的毛利润最多是1400元.(请直接写出答案)
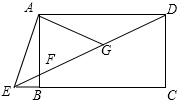 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.