题目内容
13.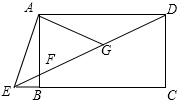 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.
分析 先证明∠ADE=∠DEC,设∠CED=x,则∠AED=2x,∠ADE=x,证明∠AED=∠AGE=2x,则AE=AG=4,由勾股定理计算AB的长即可.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=90°,
∴∠ADE=∠DEC,
设∠CED=x,则∠AED=2x,∠ADE=x,
在Rt△FAD中,G是DF的中点,DF=8,
∴AG=DG=4,
∴∠GAD=∠ADE=x,
∴∠AGE=∠GAD+∠ADE=2x,
∴∠AGE=∠AED=2x,
∴AE=AG=4,
由勾股定理得:AB=$\sqrt{A{E}^{2}-B{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 本题考查了矩形的性质,还考查了等腰三角形、直角三角形斜边中线的性质,设未知数,分别表示相关的角,根据等角对等边证明边相等,从而可以利用勾股定理计算边的长度.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
8.下列方程中,你最喜欢的一个一元二次方程是( )
| A. | $\frac{1}{4}{x^2}$-x=9 | B. | x3-x2+40=0 | C. | $\frac{4}{x-1}$=3 | D. | 3x3-2xy+y2=0 |

 AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.
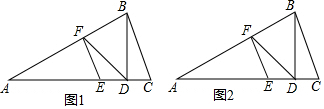
AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°. 如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.