题目内容
10.已知抛物线y=$\frac{1}{2}$x2+bx经过点A(4,0),另有一点C(1,-3),若点D在抛物线的对称轴上,且AD+CD的值最小,求点D的坐标.分析 如图,连接AC与对称轴的交点即为点D(两点之间线段最短).求出直线AC的解析式即可解决问题.
解答 解:如图,连接AC与对称轴的交点即为点D.
∵y=$\frac{1}{2}$x2+bx经过点A(4,0),
∴0=8+4b,
∴b=-2,
∴抛物线的解析式为y=$\frac{1}{2}$x2-2x,
∵A(4,0),C(1,-3),
∴直线AC的解析式为y=x-4,
∵对称轴x=2,∴y=-2,
∴点D坐标(2,-2).
点评 本题考查轴对称-最短问题,二次函数等知识,解题的关键是掌握利用两点之间线段最短解决最值问题,灵活应用待定系数法确定函数解析式,属于中考常考题型.

练习册系列答案
相关题目
19.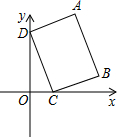 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )| A. | (2,4) | B. | ($\frac{5}{2}$,4) | C. | (3,4) | D. | (2,5) |
 AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.
AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°. 如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.