题目内容
5. 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出A1,B1,C1的坐标(直接写答案)(1,5),(1,0),(4,3).
(3)在y轴上画出一点P,使PC+PB的值最小.
分析 (1)根据由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形;
(2)根据△A1B1C1各顶点的位置,写出其坐标即可;
(3)连接BC1,交y轴于点P,连接PC,则点P即为所求,此时PC=PC1,根据两点之间线段最短,可得PC+PB的值最小.
解答 解:(1)如图所示,△A1B1C1即为所求;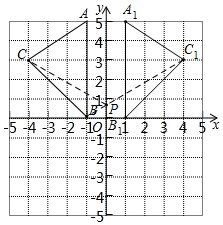
(2)由图可得,A1(1,5),B1(1,0),C1(4,3),
故答案为:(1,5),(1,0),(4,3);
(3)如图所示,连接BC1,交y轴于点P,则点P即为所求,
连接PC,则PC=PC1,根据两点之间线段最短,可得PC+PB的值最小.
点评 本题主要考查了利用轴对称变换作图以及最短距离的问题,解题时注意:凡是涉及最短距离的问题,一般要考虑线段的性质定理,运用轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列运算中正确的是( )
| A. | 2a+3a2=5a3 | B. | (-2a2)3=-8a6 | C. | a2•a3=a6 | D. | a8÷a2=a4 |

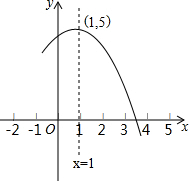 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论: 如图,菱形ABCD的对角线AC=6,BD=8,则菱形ABCD的周长为20.
如图,菱形ABCD的对角线AC=6,BD=8,则菱形ABCD的周长为20.