题目内容
17.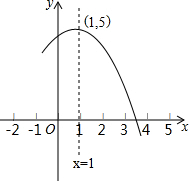 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:①a-b+c>0;
②2a+b=0;
③b2-4ac>0;
④一元二次方程ax2+bx+c=5有两个不相等的实数根.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①正确.根据x=-1时,y>0,即可判断.
②正确.根据对称轴x=-$\frac{b}{2a}$=1,即可判断.
③正确.根据抛物线与x轴有两个交点,可知△>0,即可判断.
④错误.根据抛物线的顶点坐标为(1,5),直线y=5与抛物线的只有一个交点,推出一元二次方程ax2+bx+c=5有相等的实数根,由此即可判断.
解答 解:由图象可知,x=-1时,y>0,
∴a-b+c>0,故①正确.
∵抛物线的对称轴x=1,
∴-$\frac{b}{2a}$=1,
∴-b=2a,
∴2a+b=0.故②正确.
∵抛物线与x轴有两个交点,
∴△>0,
∴b2-4ac>0,故③正确.
∵抛物线的顶点坐标为(1,5),
∴直线y=5与抛物线的只有一个交点,
∴一元二次方程ax2+bx+c=5有相等的实数根,∴④错误.
故选C.
点评 本题考查二次函数与x轴的交点、二次函数的图象与系数的关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | -$\frac{2mn}{3}$的系数是-2 | B. | 32ab3的次数是6次 | ||
| C. | x2+x-1的常数项为1 | D. | 4x2y-5x2y2+7xy是四次三项式 |
2.下列函数中,一次函数是( )
| A. | y=8x2 | B. | y=8x-1 | C. | y=x+1 | D. | y=$\frac{1}{x+1}$ |
6.下列性质中,菱形具有而矩形不一定具有的是( )
| A. | 有一个角是直角 | B. | 对边相等 | C. | 对角线互相平分 | D. | 对角线互相垂直 |
 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3). 如图是有一些完全相同的小正方体搭成的几何体分别从左面和上面看到的形状图,搭成这个几何体最多需要8个小正方体.
如图是有一些完全相同的小正方体搭成的几何体分别从左面和上面看到的形状图,搭成这个几何体最多需要8个小正方体.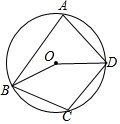 如图,A,B,C,D是⊙O上的四点,且∠C=100°,求∠BOD和∠A的度数.
如图,A,B,C,D是⊙O上的四点,且∠C=100°,求∠BOD和∠A的度数.