题目内容
15.若α,β是方程x2+px+8=0的两个不同实数根,且|α|>|β|,则下面的四个结论中不一定成立的是( )| A. | |α|>2且|β|>2 | B. | |α|+|β|>4$\sqrt{2}$ | C. | |α|>$\frac{5}{2}$或|β|>$\frac{5}{2}$ | D. | |α|>2且|β|<2$\sqrt{2}$ |
分析 由根与系数的关系得:αβ=8,
A:由特殊值法不一定成立,
B:由均值不等式,|α|+|β|>=2$\sqrt{αβ}$=4$\sqrt{2}$,一定成立,
C:反证法,否则会有|α||β|<$\frac{5}{2}×\frac{5}{2}$=$\frac{25}{4}$<8,故一定成立,
D:因为|α|>|β|,故8=|ab|<|a2|,得:|a|>2$\sqrt{2}$; 同样8=|ab|>|b2|,得|b|<2$\sqrt{2}$,一定成立.
解答 解:由根与系数的关系得:αβ=8,
A:不一定成立,比如取α=8,β=1.
B:一定成立,由均值不等式,|α|+|β|>=2$\sqrt{αβ}$=4$\sqrt{2}$,
C:一定成立,否则会有|α||β|<$\frac{5}{2}×\frac{5}{2}$=$\frac{25}{4}$<8,
D:一定成立,因为α|>|β|,故8=|αβ|<|α2|,得:|α|>2$\sqrt{2}$; 同样8=|αβ|>|β2|,得|β|<2$\sqrt{2}$,
故选:A.
点评 本题主要考查了根与系数的关系,不等式,灵活掌握不等式是解决问题的关键.

练习册系列答案
相关题目
3.方程2x2-8=0的根是( )
| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
10.下列方程是一元二次方程的是 ( )
| A. | x-y2=1 | B. | $\frac{1}{{x}^{2}}$-1=0 | C. | 5(x-1)2=3(x+2)2+2x2 | D. | $\frac{{x}^{2}}{2}$-$\frac{x-1}{3}$=0 |
7.若关于x的一元二次方程kx2-10x+3=0有一个根为3,则k的值为( )
| A. | 11 | B. | -11 | C. | 3 | D. | -3 |

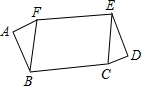 如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC.
如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC. 已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,求证:△ABE≌△ACD.
已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,求证:△ABE≌△ACD. (1)如图所示,b⊥a,c⊥a,请判断b与c的位置关系.并说明理由
(1)如图所示,b⊥a,c⊥a,请判断b与c的位置关系.并说明理由