题目内容
13．若一个直角三角形的面积为6cm2，斜边长为5cm，则该直角三角形的周长是（ ）| A． | 7cm | B． | 10cm | C． | $（5+\sqrt{37}）$cm | D． | 12cm |
分析 设直角三角形的两条直角边为a、b，由面积为6cm2，得出$\frac{1}{2}$ab=6，进一步由勾股定理得出a2+b2=52，两个式子联立求得a+b即可算出结果．
解答 解：设直角三角形的两条直角边为a、b，
则$\frac{1}{2}$ab=6，则2ab=24，
又a2+b2=52，
则（a+b）2=49，
a+b=7，
所以该直角三角形的周长是7+5=12cm．
故选：D．
点评 此题考查勾股定理的运用，三角形的面积计算方法，渗透整体思想．
练习册系列答案
阅读快车系列答案
相关题目
3．
如图，以直角三角形的三边作正方形，已知S1=9，S2=36，S3=4，正方形S的边长为8，则S4=（ ）
如图，以直角三角形的三边作正方形，已知S1=9，S2=36，S3=4，正方形S的边长为8，则S4=（ ）| A． | 12 | B． | 14 | C． | 15 | D． | 16 |
4．
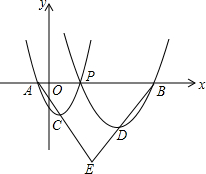如图，已知点A（-1，0），B（7，0），P是线段AB上任意一点（不含端点A，B），过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上，它们的顶点分别为C、D，射线BD与AC相交于点E．当AE=BE=5时，这两个二次函数的最小值之和等于（ ）
如图，已知点A（-1，0），B（7，0），P是线段AB上任意一点（不含端点A，B），过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上，它们的顶点分别为C、D，射线BD与AC相交于点E．当AE=BE=5时，这两个二次函数的最小值之和等于（ ）| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
如图，点A、B、C在直线l上，点P在直线l外，PB⊥l于点B，则点P到直线l的距离是线段PB的长度．
8．
如图，Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D．若AB=m，CD=n，则△ABD的面积等于（ ）
如图，Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D．若AB=m，CD=n，则△ABD的面积等于（ ）| A． | mn | B． | $\frac{1}{2}mn$ | C． | 2mn | D． | $\frac{1}{3}mn$ |
如图，射线OA的方向是北偏西60°，射线OB的方向是南偏东25°，则∠AOB=145°．
2．
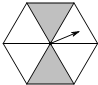如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是（ ）
如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
3．下列各式中，是最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{4a}$ | C． | $\sqrt{\frac{1}{5}}$ | D． | $\sqrt{{a}^{4}}$ |