题目内容
4.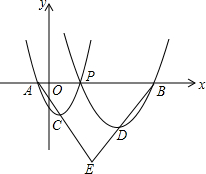 如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )
如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
分析 作CG⊥AB,EH⊥AB,DM⊥AB,根据二次函数的对称性可知AG=PG,PM=BM,根据等腰三角形的性质可知AH=BH=4从而得出AG+BM=PG+PM=$\frac{1}{2}$AB=4,再根据平行线分线段成比例定理求解即可.
解答  解:如图,由二次函数的性质,AC=PC,PD=BD,
解:如图,由二次函数的性质,AC=PC,PD=BD,
∵AE=BE=5,
∴∠ABE=∠BAE,
作CG⊥AB,EH⊥AB,DM⊥AB,
∴AH=BH=4,AG=PG,PM=BM,
∴AG+BM=PG+PM=$\frac{1}{2}$AB=4,
∵AE=BE=5,
∴EH=3,
∴$\frac{AH}{EH}$=$\frac{BH}{EH}$=$\frac{4}{3}$,
∵CG⊥AB,EH⊥AB,DM⊥AB,
∴CG∥EH∥DM,
∴$\frac{AG}{GC}$=$\frac{BM}{DM}$=$\frac{AH}{EH}$=$\frac{4}{3}$
∴AG=$\frac{4}{3}$CG,BM=$\frac{4}{3}$DM,
∴$\frac{4}{3}$CG+$\frac{4}{3}$DM=4,
∴CG+DM=3,
∴两个二次函数的最小值之和等于-3.
故选C.
点评 本题考查了二次函数的最值问题,二次函数图象的对称性,等腰三角形的性质,平行线分线段成比例定理等,求得AG+BM=PG+PM=$\frac{1}{2}$AB=4是解题的关键.

练习册系列答案
相关题目
15. 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
12.若$a=\sqrt{7}-2\sqrt{2}$,则${a^2}+\frac{1}{a^2}+2$=( )
| A. | 16 | B. | 32 | C. | -16 | D. | -32 |
9. 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
| A. | ①② | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
13.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是( )
| A. | 7cm | B. | 10cm | C. | $(5+\sqrt{37})$cm | D. | 12cm |
 如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.
如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°. 如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.
如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.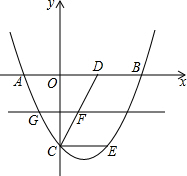 如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G.
如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G. 如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.
如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.