题目内容
3. 如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )
如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )| A. | 12 | B. | 14 | C. | 15 | D. | 16 |
分析 由正方形S的边长为8,得出S=64,由勾股定理可知:S=S1+S2+S3+S4,由此求得答案即可.
解答 解:∵正方形S的边长为8,
∴正方形S的面积为64,
由勾股定理可知:S=S1+S2+S3+S4,
∵S1=9,S2=36,S3=4,
∴S4=15.
故选:C.
点评 本题考查了勾股定理,利用面积法推导勾股定理是常用的一种方法.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个定点,点B是反比例函数y=$\frac{k-3}{x}$(y>0)的图象上一个动点,当△ABO的面积随点B的横坐标增大而减小时,则k的取值范围是( )
| A. | k<3 | B. | k≤3 | C. | k>3 | D. | k≥3 |
15. 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
12.若$a=\sqrt{7}-2\sqrt{2}$,则${a^2}+\frac{1}{a^2}+2$=( )
| A. | 16 | B. | 32 | C. | -16 | D. | -32 |
13.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是( )
| A. | 7cm | B. | 10cm | C. | $(5+\sqrt{37})$cm | D. | 12cm |
 如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.
如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.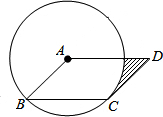 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2.