题目内容
8. 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD的面积等于( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD的面积等于( )| A. | mn | B. | $\frac{1}{2}mn$ | C. | 2mn | D. | $\frac{1}{3}mn$ |
分析 根据角平分线上的点到角的两边的距离相等可得DE=CD,然后由三角形的面积公式进行解答即可.
解答  解:如图,过点D作DE⊥AB于点E.
解:如图,过点D作DE⊥AB于点E.
∵∠C=90°,BD是∠ABC的平分线,CD=n,
∴DE=CD=n,
∵AB=m,
∴△ABD的面积是:$\frac{1}{2}$AB•DE=$\frac{1}{2}$mn.
故选:B.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
13.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是( )
| A. | 7cm | B. | 10cm | C. | $(5+\sqrt{37})$cm | D. | 12cm |
20.下列计算正确的是( )
| A. | -22=4 | B. | 32=6 | C. | (-1)3=-1 | D. | -|-1|=1 |
 如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.
如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.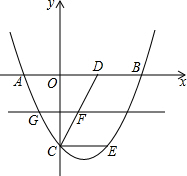 如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G.
如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G.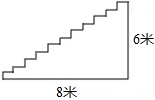 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?