题目内容
13.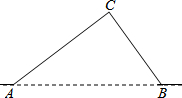 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(精确到0.1)
(sin25°≈0.42,cos25°≈0.91,$\sqrt{2}$≈1.41)
分析 (1)过点C作CD⊥AB与D,根据AC=10千米,∠CAB=25°,求出CD、AD,根据∠CBA=45°,求出BD、BC,最后根据AB=AD+BD列式计算即可,
(2)根据AC=10千米,BC=5.9千米,即可得出公路改直后该段路程比原来缩短的路程.
解答  解:(1)过点C作CD⊥AB与D,
解:(1)过点C作CD⊥AB与D,
∵AC=10千米,∠CAB=25°,
∴CD=sin∠CAB•AC=sin25°×10≈0.42×10=4.2(千米),
AD=cos∠CAB•AC=cos∠25°×10≈0.91×10=9.1(千米),
∵∠CBA=45°,
∴BD=CD=4.2(千米),
BC=$\frac{CD}{sin∠CBA}$=$\frac{4.2}{sin45°}$≈5.9(千米),
∴AB=AD+BD=9.1+4.2=13.3(千米),
(2)∵AC=10千米,BC=5.9千米,
∴公路改直后该段路程比原来缩短10+5.9-13.3=2.6千米.
点评 此题考查了解直角三角形的应用,用到的知识点是三角函数、特殊角的三角函数值,关键是作出辅助线,构造直角三角形,求出有关线段的长.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 有一条对角线平分另一条对角线的四边形是平行四边形 | |
| B. | 一组对边平行,一组对角相等的四边形是平行四边形 | |
| C. | 对角线互相垂直的平行四边形是矩形 | |
| D. | 两条对角线互相垂直且平分一组对角的平行四边形是正方形 |
 如图,AB⊥BD,CD⊥BD,AB=4,CD=6,BD=14,P为BD上一动点,当PB为何值时△ABP与△CDP相似.
如图,AB⊥BD,CD⊥BD,AB=4,CD=6,BD=14,P为BD上一动点,当PB为何值时△ABP与△CDP相似.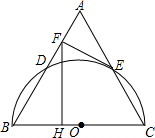 如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、E,过点E作EF⊥AB,垂足为点F,过F作FH⊥BC,垂足为H.若AB=8,则FH的长为3$\sqrt{3}$.
如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、E,过点E作EF⊥AB,垂足为点F,过F作FH⊥BC,垂足为H.若AB=8,则FH的长为3$\sqrt{3}$. 如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,且AD=BE=CF
如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,且AD=BE=CF