题目内容
4.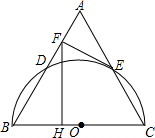 如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、E,过点E作EF⊥AB,垂足为点F,过F作FH⊥BC,垂足为H.若AB=8,则FH的长为3$\sqrt{3}$.
如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、E,过点E作EF⊥AB,垂足为点F,过F作FH⊥BC,垂足为H.若AB=8,则FH的长为3$\sqrt{3}$.
分析 首先连接BE,由BC为直径,根据直径所对的圆周角是直角,可求得∠BEC=90°,然后由三线合一,求得AE的长,继而由EF⊥AB,求得AF的长,又由FH⊥BC,求得FH的长.
解答  解:连接BE,
解:连接BE,
∵BC为直径,
∴∠BEC=90°,
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,AE=EC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4,
∵EF⊥AB,
∴AF=AE•cos60°=4×$\frac{1}{2}$=2,
∴BF=AB-AF=6,
∵FH⊥BC,
∴FH=BF•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 此题考查了圆周角定理以及三角函数的定义.注意掌握辅助线的作法.

练习册系列答案
相关题目
14.A、B、C、D、E五名同学在一次数学测验中的平均成绩是80分,而A、B、C三人的平均成绩是78分,下列说法一定正确的是( )
| A. | D、E的成绩比其他三人都好 | |
| B. | D、E两人的平均成绩是83分 | |
| C. | 五人成绩的中位数一定是其中一人的成绩 | |
| D. | 五人的成绩的众数一定是80分 |
12.根据某班40名同学一周的体育锻炼情况绘制了如下统计表,那么关于该班40名同学一周的体育锻炼时间的中位数是8.5小时.
| 时间(小时) | 7 | 8 | 9 | 10 |
| 人数(人) | 3 | 17 | 14 | 6 |
19.据国家统计局发布的数据显示,2015年一季度我国国内生产总值约为14060000000000元,这个数字用科学记数法表示为( )
| A. | 1.406×1013 | B. | 14.06×1012 | C. | 1.406×1012 | D. | 140.6×1011 |
16.使$\sqrt{{x}^{2}+1}$在实数范围内有意义的x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≥-1 | D. | x为任意实数 |
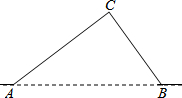 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.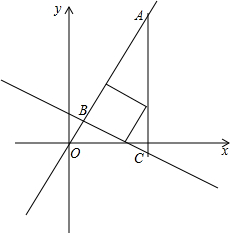 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+$\frac{5}{2}$交直线y=kx(k>0)于点B,平行于y轴的直线x=7交它们于点A、C,且AC=15.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+$\frac{5}{2}$交直线y=kx(k>0)于点B,平行于y轴的直线x=7交它们于点A、C,且AC=15.