题目内容
7.如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.(1)在图1中画一个以线段AB为一边的平行四边形ABCD,点C、D均在小正方形的顶点上,且平行四边形ABCD的面积为10;
(2)在图2中画一个钝角三角形ABE,点E在小正方形的顶点上,且三角形ABE的面积为4,tan∠AEB=$\frac{1}{3}$.请直接写出BE的长.
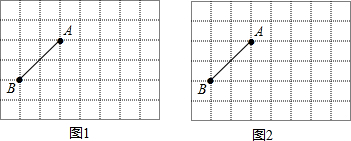
分析 (1)由图可知A、B间的垂直方向长为2,要使构建平行四边形ABCD的面积为10,则可以在A的水平方向取一条长为5的线段,可得点C;
(2)由图可知A、B间的垂直方向长为2,要使构建的钝角三角形ABE面积为4,则可以在A的水平方向取一条长为4的线段,可得点E,且tan∠AEB=$\frac{1}{3}$,BE的长可以根据勾股定理求得.
解答 解:(1)如图1所示;
(2)如图2所示;
BE=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
点评 本题考查勾股定理运用及面积计算方法等,灵活利用数据之间的联系,结合图形解决问题是关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
12.下列等式中,从等号左边到右边的变形是因式分解的是( )
| A. | x2-9+8x=(x-3)(x+3)+8x | B. | -5x2y3=-5xy•(xy2) | ||
| C. | x2-4x-5=x(x-4-$\frac{5}{x}$) | D. | -x2+2xy=-x(x-2y) |
 已知:在△ABC中,∠B=∠C,在△ADE中∠ADE=∠AED,∠BAD=40°,求:∠EDC的度数.
已知:在△ABC中,∠B=∠C,在△ADE中∠ADE=∠AED,∠BAD=40°,求:∠EDC的度数.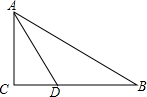 如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长.
如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长. 由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由.
由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由. 如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2.
如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2.