题目内容
8.(1)解分式方程:$\frac{1}{2-x}-2=\frac{1-x}{x-2}$.(2)先分解因式,再求值:($\frac{x+y}{3}$)2-($\frac{x-y}{3}$)2,其中x=-$\frac{3}{4}$,y=3.
(3)先化简,再求值:$\frac{{x}^{2}-4}{{x}^{2}-4x+4}÷\frac{x+2}{x+1}-\frac{x}{x-2}$,其中x=2$-\sqrt{2}$.
分析 (1)先把分式方程化为整式方程求出x的值,再代入最减公分母进行检验即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x、y的值代入进行计算即可;
(3)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)去分母得,-1-2(x-2)=1-x,解得x=2,
把x=2代入公分母x-2得,2-2=0,
故x=2是分式方程的增根,原分式方程无解;
(2)原式=($\frac{x+y}{3}$-$\frac{x-y}{3}$)($\frac{x+y}{3}$+$\frac{x-y}{3}$)
=$\frac{x+y-x+y}{3}$•$\frac{x+y+x-y}{3}$
=$\frac{2y}{3}$•$\frac{2x}{3}$
=$\frac{4xy}{9}$,
当x=-$\frac{3}{4}$,y=3时,原式=$\frac{4×(-\frac{3}{4})×3}{9}$=$\frac{-3×3}{9}$=-1;
(3)原式=$\frac{x+2}{x-2}$•$\frac{x+1}{x+2}$-$\frac{x}{x-2}$
=$\frac{x+1}{x-2}$-$\frac{x}{x-2}$
=$\frac{1}{x-2}$,
当x=2-$\sqrt{2}$时,原式=$\frac{1}{2-\sqrt{2}-2}$=-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
3.分解因式2x2-4x的最终结果是( )
| A. | 2(x2-2x) | B. | x(2x2-4) | C. | 2x(x-2) | D. | 2x(x-4) |
20.一扇形的半径等于已知圆的半径的3倍,且它的面积等于该圆的面积,则这一扇形的圆心角为( )
| A. | 20° | B. | 120° | C. | 100° | D. | 40° |
 已知:在△ABC中,∠B=∠C,在△ADE中∠ADE=∠AED,∠BAD=40°,求:∠EDC的度数.
已知:在△ABC中,∠B=∠C,在△ADE中∠ADE=∠AED,∠BAD=40°,求:∠EDC的度数. 如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2.
如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2.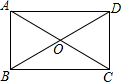 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$.