题目内容
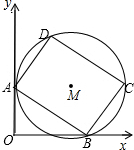 如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变.
如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变.(1)问
| OA |
| OB |
(2)问OB为多少时,⊙H与x轴相切;
(3)当
| OA |
| OB |
| 1 |
| 2 |
考点:圆的综合题
专题:
分析:(1)根据题意得出当AC⊥y轴时,点C距y轴最远,进而利用△AOB∽△CBA,进而求出答案;
(2)当△AOB∽△DAB时,∠OAB=∠CAB,进而利用,⊙M与x轴相切,即
=
,求出BO的长即可;
(3)过点C作CK⊥x轴于K,得出OA=
,OB=
,进而得出cos∠ABO=cos∠BCK,进而求出CK与OK的长,进而得出答案.
(2)当△AOB∽△DAB时,∠OAB=∠CAB,进而利用,⊙M与x轴相切,即
| BO |
| AB |
| AD |
| BD |
(3)过点C作CK⊥x轴于K,得出OA=
8
| ||
| 5 |
16
| ||
| 5 |
解答:解:(1)∵矩形ABCD是⊙M的内接矩形,
∴∠A=∠B=90°,
∴AC是⊙M的直径,
∴当AC⊥y轴时,点C距y轴最远,
∴AC∥OB,
∴∠ABC=∠CBA,即∠AOB=∠ABC=90°,
∴△AOB∽△CBA,
∴
=
=
时,点C距y轴最远;
(2)由(1)可知,∠A=90°,
∴BD是⊙M的直径,
当△AOB∽△DAB时,∠OAB=∠CAB,
 ∵∠OAB+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠DBA+∠ABO=90°,
∴BD⊥x轴,∴⊙M与x轴相切,即
=
,
在Rt△BAD中,由勾股定理可知:
BD=10,∴
=
,
∴BO=4.8,
∴当OB=4.8时,⊙M与x轴相切;
(3)过点C作CK⊥x轴于K,
在Rt△ABO中,AB=8,
=
,∴OA=
,OB=
,
∵∠B=90°,
∴∠ABO+∠CBK=∠CBK+∠BCK=90°,
∴∠ABO=∠BCK,
即cos∠ABO=cos∠BCK,
∴
=
,
∴
=
,
解得;CK=
,
∵tan∠ABO=tan∠BCK=
,
∴BK=
CK=
,
∴OK=
+
=
,
∴C(
,
).
∴∠A=∠B=90°,
∴AC是⊙M的直径,
∴当AC⊥y轴时,点C距y轴最远,
∴AC∥OB,
∴∠ABC=∠CBA,即∠AOB=∠ABC=90°,
∴△AOB∽△CBA,
∴
| OA |
| OB |
| 6 |
| 8 |
| 3 |
| 4 |
(2)由(1)可知,∠A=90°,
∴BD是⊙M的直径,
当△AOB∽△DAB时,∠OAB=∠CAB,
 ∵∠OAB+∠ABO=90°,
∵∠OAB+∠ABO=90°,∴∠DBA+∠ABO=90°,
∴BD⊥x轴,∴⊙M与x轴相切,即
| BO |
| AB |
| AD |
| BD |
在Rt△BAD中,由勾股定理可知:
BD=10,∴
| BO |
| 8 |
| 6 |
| 10 |
∴BO=4.8,
∴当OB=4.8时,⊙M与x轴相切;
(3)过点C作CK⊥x轴于K,
在Rt△ABO中,AB=8,
| OA |
| OB |
| 1 |
| 2 |
8
| ||
| 5 |
16
| ||
| 5 |
∵∠B=90°,
∴∠ABO+∠CBK=∠CBK+∠BCK=90°,
∴∠ABO=∠BCK,
即cos∠ABO=cos∠BCK,
∴
| OB |
| AB |
| CK |
| BC |
∴
| ||||
| 8 |
| CK |
| 6 |
解得;CK=
| 12 |
| 5 |
| 5 |
∵tan∠ABO=tan∠BCK=
| 1 |
| 2 |
∴BK=
| 1 |
| 2 |
| 6 |
| 5 |
| 5 |
∴OK=
| 16 |
| 5 |
| 5 |
| 6 |
| 5 |
| 5 |
22
| ||
| 5 |
∴C(
| 22 |
| 5 |
| 5 |
| 12 |
| 5 |
| 5 |
点评:此题主要考查了圆的综合以及相似三角形的判定与性质和锐角三角函数关系等知识,利用切线的性质以及锐角三角函数关系是解题关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图是由五个完全相同的正方体堆成的物体,则这一物体的俯视图是( )
如图是由五个完全相同的正方体堆成的物体,则这一物体的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
 分析,绘制成频数分布步和频数分布直方图,请你根据图表提供的信息,解答下列问题:
分析,绘制成频数分布步和频数分布直方图,请你根据图表提供的信息,解答下列问题: