题目内容
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.

(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.

考点:四边形综合题
专题:压轴题
分析:(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以
=
,从而求得PQ,由PN∥EG,得出
=
,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以
| PE |
| CE |
| PQ |
| CA |
| CP |
| CE |
| PN |
| EG |
解答:(1)证明:由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,
∴△DEC≌△EDA(SSS);
(2)解:如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=
,
即DF=
.
(3)解:如图2,由矩形PQMN的性质得PQ∥CA
∴
=
又∵CE=3,AC=
=5
设PE=x(0<x<3),则
=
,即PQ=
x
过E作EG⊥AC于G,则PN∥EG,
∴
=
又∵在Rt△AEC中,EG•AC=AE•CE,解得EG=
,
∴
=
,即PN=
(3-x),
设矩形PQMN的面积为S,
则S=PQ•PN=-
x2+4x=-
(x-
)2+3(0<x<3)
所以当x=
,即PE=
时,矩形PQMN的面积最大,最大面积为3.
在△ADE与△CED中,
|
∴△DEC≌△EDA(SSS);
(2)解:如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=
| 7 |
| 8 |
即DF=
| 7 |
| 8 |
(3)解:如图2,由矩形PQMN的性质得PQ∥CA

∴
| PE |
| CE |
| PQ |
| CA |
又∵CE=3,AC=
| AB2+BC2 |
设PE=x(0<x<3),则
| x |
| 3 |
| PQ |
| 5 |
| 5 |
| 3 |
过E作EG⊥AC于G,则PN∥EG,
∴
| CP |
| CE |
| PN |
| EG |
又∵在Rt△AEC中,EG•AC=AE•CE,解得EG=
| 12 |
| 5 |
∴
| 3-x |
| 3 |
| PN | ||
|
| 4 |
| 5 |
设矩形PQMN的面积为S,
则S=PQ•PN=-
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
所以当x=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了全等三角形的判定和性质,勾股定理的应用,平行线分线段成比例定理.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

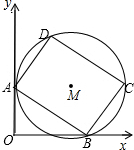 如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变.
如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变. 如图,在△ABC中,BD⊥AC,AB=6,AC=5
如图,在△ABC中,BD⊥AC,AB=6,AC=5 如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(
如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为( 如图,反比例函数y1=
如图,反比例函数y1=