题目内容
如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.
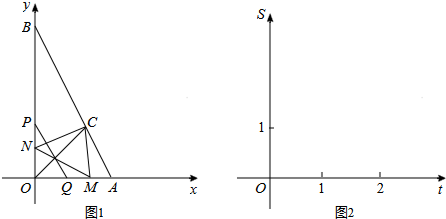
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.
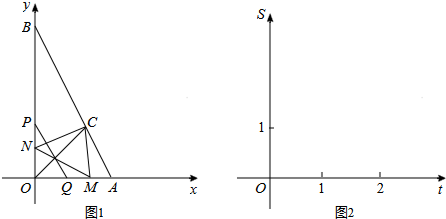
考点:相似形综合题
专题:代数几何综合题,压轴题
分析:(1)如答图1,作辅助线,由比例式求出点D的坐标;
(2)①所求函数关系式为分段函数,需要分类讨论.
答图2-1,答图2-2表示出运动过程中重叠部分(阴影)的变化,分别求解;
②画出函数图象,由两段抛物线构成.观察图象,可知当t=1时,S有最大值.
(2)①所求函数关系式为分段函数,需要分类讨论.
答图2-1,答图2-2表示出运动过程中重叠部分(阴影)的变化,分别求解;
②画出函数图象,由两段抛物线构成.观察图象,可知当t=1时,S有最大值.
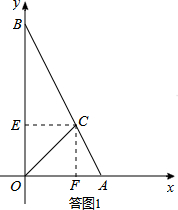
解答:解:(1)如答图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意,易知四边形OECF为正方形,设正方形边长为x.
∵CE∥x轴,
∴
=
,即
=
,解得x=
.
∴C点坐标为(
,
);
∵PQ∥AB,
∴
=
,即
=
,
∴OP=2OQ.
∵P(0,2t),
∴Q(t,0).
∵对称轴OC为第一象限的角平分线,
∴对称点坐标为:M(2t,0),N(0,t).
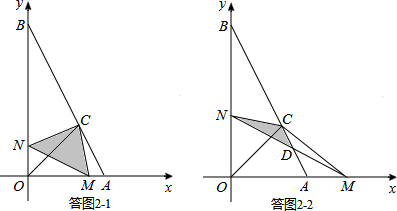
(2)①当0<t≤1时,如答图2-1所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON-S△OMN
=(S△COM+S△CON)-S△OMN
=(
•2t×
+
•t×
)-
•2t•t
=-t2+2t;
当1<t<2时,如答图2-2所示,点M在OA的延长线上,设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,将M(2t,0)、N(0,t)代入得
,
解得
,
∴y=-
x+t;
同理求得直线AB的解析式为:y=-2x+4.
联立y=-
x+t与y=-2x+4,求得点D的横坐标为
.
S△CDN=S△BDN-S△BCN
=
(4-t)•
-
(4-t)×
=
t2-2t+
.
综上所述,S=
.
②画出函数图象,如答图2-3所示:
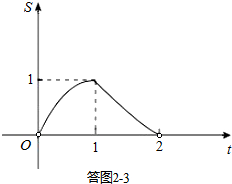
观察图象,可知当t=1时,S有最大值,最大值为1.
由题意,易知四边形OECF为正方形,设正方形边长为x.

∵CE∥x轴,
∴
| BE |
| OB |
| CE |
| OA |
| 4-x |
| 4 |
| x |
| 2 |
| 4 |
| 3 |
∴C点坐标为(
| 4 |
| 3 |
| 4 |
| 3 |
∵PQ∥AB,
∴
| OP |
| OB |
| OQ |
| OA |
| OP |
| 4 |
| OQ |
| 2 |
∴OP=2OQ.
∵P(0,2t),
∴Q(t,0).
∵对称轴OC为第一象限的角平分线,
∴对称点坐标为:M(2t,0),N(0,t).
(2)①当0<t≤1时,如答图2-1所示,点M在线段OA上,重叠部分面积为S△CMN.

S△CMN=S四边形CMON-S△OMN
=(S△COM+S△CON)-S△OMN
=(
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
=-t2+2t;
当1<t<2时,如答图2-2所示,点M在OA的延长线上,设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,将M(2t,0)、N(0,t)代入得
|
解得
|
∴y=-
| 1 |
| 2 |
同理求得直线AB的解析式为:y=-2x+4.
联立y=-
| 1 |
| 2 |
| 8-2t |
| 3 |
S△CDN=S△BDN-S△BCN
=
| 1 |
| 2 |
| 8-2t |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
=
| 1 |
| 3 |
| 8 |
| 3 |
综上所述,S=
|
②画出函数图象,如答图2-3所示:

观察图象,可知当t=1时,S有最大值,最大值为1.
点评:本题是运动型综合题,涉及二次函数与一次函数、待定系数法、相似、图形面积计算、动点问题函数图象等知识点.难点在于第(2)问,正确地进行分类讨论,是解决本题的关键.

练习册系列答案
相关题目
 如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,| 1 |
| 2 |
| A、40°或80° |
| B、50°或100° |
| C、50°或110° |
| D、60°或120° |
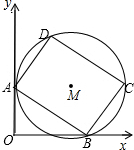 如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变.
如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变. 如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(
如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(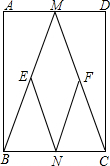 已知如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是BM,CM的中点.
已知如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是BM,CM的中点. 如图,反比例函数y1=
如图,反比例函数y1=