题目内容
5.如图1,在平面直角坐标系中,点A、B、C的坐标分别为(-8,0),(-5,0),(0,-8),点P,E分别从点A,B同时出发沿x轴正方向运动,同时点D从点C出发沿y轴正方向运动.以PD,PE为邻边构造平行四边形EPDF,已知点P,D的一点速度均为每秒2个单位,点E的运动速度为每秒1个单位,运动时间为t秒.(1)当0<t<3时,PE=3-t(用含t的代数式表示);
(2)记平行四边形的面积为S,当S=12时,求t的值;
(3)如图2,当0<t<4时,过点P的作抛物线y=ax2+bx+c交x轴于另一点为H(点H在点P的右侧),若PH=6,且该二次函数的最大值不变均为$\frac{9}{4}$.
①当t=2时,试判断点F是否恰好落在抛物线y=ax2+bx+c上?并说明理由;
②若点D关于直线EF的对称点Q恰好落在抛物线y=ax2+bx+c,请直接写出t的值.
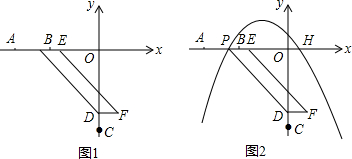
分析 (1)根据题意,求出OP及OE的长度,即可求得PE的长度;
(2)根据平行四边形的面积=底×高,以PE为底,OD为高,即可解答;
(3)根据点P的坐标,PH=6,求出点H的坐标,然后求出抛物线的顶点坐标,用含t的式子表示出函数的解析式;
①求出当t=2时,点B,E,D,F的坐标,将点F的横坐标代入解析式,看求出的y的值是否与点F的纵坐标相等,即可判断;
②根据对称,求出点Q的坐标,将点Q的坐标代入抛物线,即可求出t的值.
解答 解:(1)根据题意,得:OP=8-2t,OE=5-t,
∴PE=OP-OE=(8-2t)-(5-t)=3-t;
故答案为:3-t;
(2)当0<t<3时,
根据题意,得:OD=8-2t,
∴S=(3-t)(8-2t)=2t2-14t+24,
当S=12时,2t2-14t+24=12,解得:t1=1,t2=6;
当t=3时,点P与点E重合,不能围成平行四边形;
当t>3时,根据题意,得:PE=5-t-8+2t=t-3,OD=8-2t,
∴S=(t-3)(8-2t)=-2t2+14t-24,
当S=12时,-2t2+14t-24=12,解得:t1=-2(不合题意,舍去),t2=9,
综上所述,当S=12时,求t的值为1或6或9;
(3)当0<t<4时,点P(2t-8,0),
∵PH=6,
∴点H(2t-2,0),
∴抛物线对称轴为:x=$\frac{2t-8+2t-2}{2}=2t-5$,
设抛物线解析式为:$y=a(x-2t+5)^{2}+\frac{9}{4}$,
根据点P(2t-8,0)在抛物线上,可得:$a(2t-8-2t+5)^{2}+\frac{9}{4}=0$,解得:a=$-\frac{1}{4}$,
∴抛物线解析式为:y=$-\frac{1}{4}(x-2t+5)^{2}+\frac{9}{4}$;
①当t=2时,PE=3-t=3-2=1,点D的纵坐标为2t-8,即点D(0,-4),
根据四边形PEFD是平行四边形,可得:DF=PE=1,
∴点F(1,-4),
当x=1时,y=$-\frac{1}{4}×(1-4+5)^{2}+\frac{9}{4}=\frac{5}{4}$,
∴点F不在抛物线y=$-\frac{1}{4}(x-2t+5)^{2}+\frac{9}{4}$上;
②t的值为1或$\frac{35}{9}$.
如图,
作点D关于EF的对称点点Q,连接QG,QF,
∵OP=OD,
∴∠ODP=45°,
∴∠FGD=45°,即△DGF是等腰直角三角形,
易证四边形FDGQ是正方形,
∴点Q(3-t,t-5),
根据点Q在抛物线上,可得:$-\frac{1}{4}(3-t-2t+5)^{2}+\frac{9}{4}=t-5$,
解得:t1=1,t2=$\frac{35}{9}$.
点评 本题主要考查二次函数的综合应用,前两个小题比较简单,第三小题,能用含t的式子表示出函数的解析式是解决①②小题的关键;第②小题中,根据点D对称的点Q与点F,G正好围成一个正方形,是解决第②小题的一个突破点.

| A. | $x>\frac{1}{2}$ | B. | $x≥\frac{1}{2}$ | C. | $x<\frac{1}{2}$ | D. | $x≠\frac{1}{2}$ |
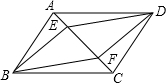 如图,在?ABCD中,E、F为对角线AC上两点,且AE=CF.
如图,在?ABCD中,E、F为对角线AC上两点,且AE=CF.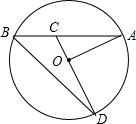 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
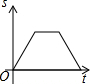
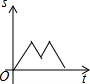
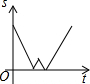
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD. 星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
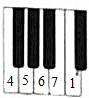 如图是钢琴键盘的一部分,若从4开始,依次弹出4,5,6,7,1,4,5,6,7,1,…,按照上述规律弹到第2016个音符是4.
如图是钢琴键盘的一部分,若从4开始,依次弹出4,5,6,7,1,4,5,6,7,1,…,按照上述规律弹到第2016个音符是4. 如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$.
如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$.