题目内容
3.先化简,再求代数式($\frac{1}{x}$+$\frac{x+1}{x}$)÷$\frac{x+2}{{x}^{2}+x}$的值,其中x=cos30°+$\frac{1}{2}$.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x+2}{x}$•$\frac{x(x+1)}{x+2}$
=x+1,
∵x=cos30°+$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$,
∴原式=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$+1=$\frac{\sqrt{3}+3}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
8.下列由左到右的变形,属于因式分解的是( )
| A. | (x+3y)(x-3y)=x2-9y | B. | x2-3x+2=(x-1)(x-2) | ||
| C. | 3x2+6x-1=3x(x+2)-1 | D. | (x-2y)2=x2-4xy+4y2 |
12.如果a>b,则下列不等式一定成立的是( )
| A. | 1-a>1-b | B. | -a>-b | C. | ac>bc | D. | a-2>b-2 |
 某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下: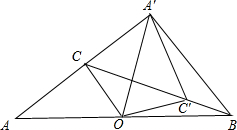 如图,已知钝角三角形ABC,∠A=36°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,连接BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为18°.
如图,已知钝角三角形ABC,∠A=36°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,连接BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为18°.