题目内容
17. 如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.
如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.
分析 连接OC、OE,由同底等高的三角形面积相等结合反比例函数系数k的几何意义,即可得出S△OBE=S△ABE=$\frac{1}{2}$×|-6|=3、S△OCD=S△BCD=$\frac{1}{2}$×8=4,再将其代入S阴影=S△ABE+S△BCD中,即可求出阴影部分的总面积.
解答 解:连接OC、OE,如图所示.
∵CD∥y轴,BE∥x轴,
∴S△OBE=S△ABE=$\frac{1}{2}$×|-6|=3,S△OCD=S△BCD=$\frac{1}{2}$×8=4,
∴S阴影=S△ABE+S△BCD=3+4=7.
故答案为:7.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数系数k的几何意义以及三角形的面积,由三角形的面积结合反比例函数系数k的几何意义找出S△OBE=S△ABE=$\frac{1}{2}$×|-6|=3、S△OCD=S△BCD=$\frac{1}{2}$×8=4是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
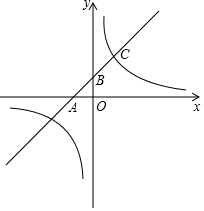 已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC.
已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC.

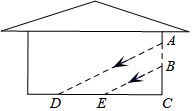 如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.
如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.