题目内容
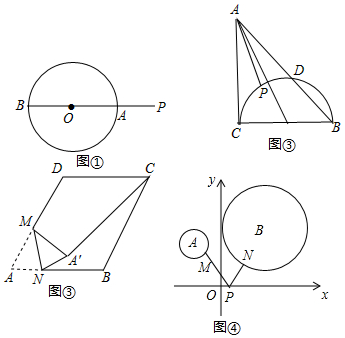
5.如图,菱形ABCD,BC∥x轴,A,B两点纵坐标分别为3和1,且菱形ABCD的面积为4$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过A、B两点.(1)求k的值;
(2)点P在双曲线上,连OP,PE∥x轴,点F在x轴上,且OP=EF,PM⊥x轴于M点,PE=2OM,求S四边形OPEF;
(3)设t=OM+PM,求t的最小值,并求此时P点的坐标.

分析 (1)先求出点A,B的坐标,得出AB,由菱形的性质得出AD=AB,最后用菱形的面积建立方程求解即可;
(2)先设出点P的坐标,进而得出OM,PM,PE,再判断出四边形OPEF是等腰梯形,最后用等腰梯形的面积公式即可得出结论;
(3)先设出点P的坐标,得出t,进而判断出|n|=|$\frac{k}{n}$|时,t最小即可得出结论.
解答 解:(1)∵A,B两点纵坐标分别为3和1,且在反比例函数y=$\frac{k}{x}$上,
∴A($\frac{k}{3}$,3),B(k,1),
∴AB=$\sqrt{(\frac{k}{3}-k)^{2}+(3-1)^{2}}$=$\frac{2}{3}$$\sqrt{{k}^{2}+9}$,
∵四边形ABCD是菱形,
∴AD=AB=$\frac{2}{3}$$\sqrt{{k}^{2}+9}$,
∵菱形ABCD的面积为4$\sqrt{2}$,
∴AD×2=$\frac{2}{3}$$\sqrt{{k}^{2}+9}$×2=4$\sqrt{2}$,
∴k=-3或k=3;
(2)∵反比例函数的解析式为y=$\frac{k}{x}$,
设P(m,$\frac{k}{m}$),
∴OM=|m|,PM=|$\frac{3}{m}$|,
∴PE=2OM=2|m|,
∵PE∥x轴,PE≠OF,OP=EF,
∴四边形OPEF是等腰梯形,
∴S四边形OPEF=$\frac{1}{2}$(PE+OF)•PM=$\frac{1}{2}$(2OM+OM+2OM+OM)•PM=3OM•PM=3×|m|×|$\frac{k}{m}$|=3|k|,
由(1)知,k=±3,S四边形OPEF=9;
(3)设P(n,$\frac{k}{n}$),
∴OM=|n|,PM=|$\frac{k}{n}$|,
∴t=OM+PM=|n|+|$\frac{k}{n}$|,
当且仅当|n|=|$\frac{k}{n}$|时,t最小=2$\sqrt{|n|×|\frac{k}{n}|}$=2$\sqrt{3}$,
即:n2=|k|,
∵k=±3,
∴n=±$\sqrt{3}$,
∴P($\sqrt{3}$,$\sqrt{3}$),或($\sqrt{3}$,-$\sqrt{3}$)或(-$\sqrt{3}$,$\sqrt{3}$)或(-$\sqrt{3}$,-$\sqrt{3}$).
点评 此题是反比例函数综合题,主要考查了待定系数法,菱形的性质,菱形的面积公式,梯形的面积公式,极值确定,解(1)的关键是用菱形的面积建立方程求解出k,解(2)的关键是四边形OPEF是等腰梯形,解(3)的关键是得出t=|n|+|$\frac{k}{n}$|,是一道中等难度的中考常考题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:| 组别 | 身高(cm) |
| A | 150≤x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | 170≤x<175 |
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
| A. | ①② | B. | ①④ | C. | ②④ | D. | ③④ |

 如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.
如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.