题目内容
18.边长为1的正六边形的边心距是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 连接OA、OB,根据正六边形的性质求出∠AOB,得出等边三角形OAB,求出OA、AM的长,根据勾股定理求出即可.
解答 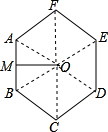 解:连接OA、OB、OC、OD、OE、OF,
解:连接OA、OB、OC、OD、OE、OF,
∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴∠AOB=360°÷6=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=1,
∵OM⊥AB,
∴AM=BM=$\frac{1}{2}$,
在△OAM中,由勾股定理得:OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\frac{\sqrt{3}}{2}$.
故选C.
点评 本题主要考查对正多边形与圆,勾股定理,等边三角形的性质和判定等知识点的理解和掌握,能求出OA、AM的长是解此题的关键.

练习册系列答案
相关题目
3.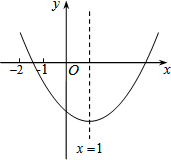 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②2a-b=0;③abc>0;④8a+c>0;⑤9a+3b+c<0,
其中正确结论的个数是( )
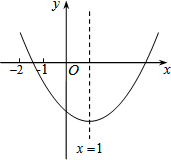 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②2a-b=0;③abc>0;④8a+c>0;⑤9a+3b+c<0,
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (3a2)3=9a6 | C. | 50÷5-2=$\frac{1}{25}$ | D. | $\sqrt{8}$-$\sqrt{50}$=-3$\sqrt{2}$ |
8.下列运算正确的是( )
| A. | a2•a2=2a2 | B. | a2+a2=a4 | C. | (1+2a)2=1+2a+4a2 | D. | (-a+1)(a+1)=1-a2 |
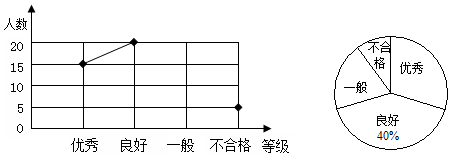
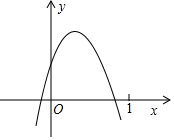 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )