题目内容
1. 如图,AB是⊙O的直径,且AB=10,弦CD⊥AB于点E,G是一动点,连结AD,AG,GD,BC.
如图,AB是⊙O的直径,且AB=10,弦CD⊥AB于点E,G是一动点,连结AD,AG,GD,BC.(1)若BE=2,求弦CD的长;
(2)若G是$\widehat{AC}$上任意一动点,请找出图中和∠G相等的角(不在原图中添加线段或字母),并说明理由;
(3)若G是⊙O及⊙O内的任意一动点,请在图中画出使△ADG和△CEB相似的所有点G.
分析 ( )1)如图1中,连接AC、BC.根据相交弦定理以及垂径定理可得,AE•EB=EC•ED,EC2=8×2=16,由此即可解决问题.
(2)结论:∠ADC=∠AGD.因为AB垂直平分CD,推出AC=AD,推出∠ACD=∠ADC,由∠AGC=∠ACD,即可证明.
(3)根据题意以及相似三角形的条件即可画出点G.
解答 解:(1)如图1中,连接AC、BC.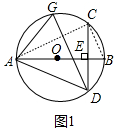
∵AB是直接,
∴∠ACB=90°,
∵AB⊥BC,
∴EC=ED,∠AEC=∠CEB=90°,
∵AE•EB=EC•ED,
∴EC2=8×2=16,
∴EC=4,
∴CD=2EC=8.
(2)结论:∠ADC=∠AGD.
理由:∵AB垂直平分CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠AGC=∠ACD,
∴∠ADC=∠AGD.
(3)如图2中,满足条件的点G有三个,如图所示.
点评 本题考查圆综合题、相交弦定理、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,考虑问题要全面,不能漏解,属于中考常考题型.

练习册系列答案
相关题目
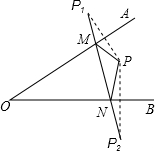 如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连结P1P2交OA于M,交OB于N,△PMN的周长为12,则P1P2长为12.
如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连结P1P2交OA于M,交OB于N,△PMN的周长为12,则P1P2长为12.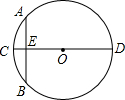 “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( ) 阅读解题过程,回答问题.
阅读解题过程,回答问题.