题目内容
13．
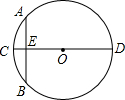“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问锯几何？”用现代的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意，CD长为（ ）| A． | 12寸 | B． | 13寸 | C． | 24寸 | D． | 26寸 |
分析 根据垂径定理和勾股定理求解．
解答 
解：连接OA，如图所示，
设直径CD的长为2x，则半径OC=x，
∵CD为⊙O的直径，弦AB⊥CD于E，AB=10寸，
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5寸，
连接OA，则OA=x寸，
根据勾股定理得x2=52+（x-1）2，
解得x=13，
CD=2x=2×13=26（寸）．
故选D．
点评 本题考查了垂径定理和勾股定理．正确的作出辅助线是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．多项式4ab2+8ab2-12ab的公因式是（ ）
| A． | 4ab | B． | 2ab | C． | 3ab | D． | 5ab |
4．若m辆客车及n个人，若每辆汽车乘40人，则还有10人不能上车；若每辆客车乘43人，则只有1人不能上车，有下列四个等式：
（1）40m+10=43m+1；（2）$\frac{n+10}{40}$=$\frac{n+1}{43}$；（3）$\frac{n-10}{40}$=$\frac{n-1}{43}$；（4）40m-10=43m-1，
其中正确的是（ ）
（1）40m+10=43m+1；（2）$\frac{n+10}{40}$=$\frac{n+1}{43}$；（3）$\frac{n-10}{40}$=$\frac{n-1}{43}$；（4）40m-10=43m-1，
其中正确的是（ ）
| A． | （1）（2） | B． | （2）（4） | C． | （1）（3） | D． | （3）（4） |
如图，AB是⊙O的直径，且AB=10，弦CD⊥AB于点E，G是一动点，连结AD，AG，GD，BC．
如图，在长方形ABCD中，AB=10厘米，BC=6厘米，点P沿AB边从点A开始向点B以2厘米/秒的速度移动；点Q沿DA边从点D开始向点A以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么：
5．
如图所示，直线y=kx+b（k≠0）与x轴交于点（-5，0），则关于x的方程kx+b=0的解为x=（ ）
如图所示，直线y=kx+b（k≠0）与x轴交于点（-5，0），则关于x的方程kx+b=0的解为x=（ ）| A． | -5 | B． | -4 | C． | 0 | D． | 1 |
2．在同一时刻的太阳光下，小刚的影子比小红的影子长，那么，在晚上同一路灯下，（ ）
| A． | 小刚的影子比小红的长 | B． | 小刚的影子比小红的影子短 | ||
| C． | 小刚跟小红的影子一样长 | D． | 不能够确定谁的影子长 |