题目内容
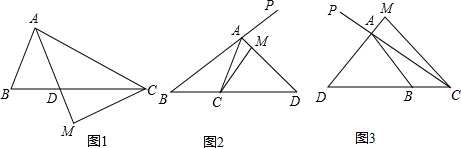
16.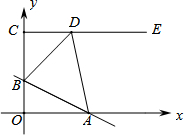 如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.
如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.
分析 分三种情况讨论:
①当∠ABD=90°时,证得△DBC≌△BAO,得出BC=OA,即4-b=2b,求得b=$\frac{4}{3}$;
②当∠ADB=90°时,作AF⊥CE于F,同理证得△BDC≌△DAF,得出BC=DF,即2b-4=4-b,求得b=$\frac{8}{3}$;
③当∠DAB=90°时,作DF⊥OA于F,同理证得△AOB≌△DFA,得出OA=DF,即2b=4,解得b=2.
解答 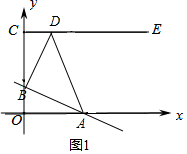 解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
∴∠DBC=∠BAO,
由直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
∵点C(0,4),
∴OC=4,
∴BC=4-b,
在△DBC和△BAO中,
$\left\{\begin{array}{l}{∠DBC=∠BAO}\\{∠DCB=∠AOB}\\{BD=AB}\end{array}\right.$
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4-b=2b,
∴b=$\frac{4}{3}$;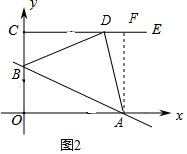 ②当∠ADB=90°时,如图2,
②当∠ADB=90°时,如图2,
作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b-4,
∵BC=4-b,
∴2b-4=4-b,
∴b=$\frac{8}{3}$;
③当∠DAB=90°时,如图3,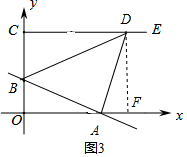
作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.
故答案为$\frac{4}{3}$或$\frac{8}{3}$或2.
点评 本题考查了一次函数图象上点的坐标特征,等腰直角三角形的性质,三角形全等的判定和性质,作出辅助性构建求得三角形上解题的关键.

 如图所示,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发.沿这条曲线向右运动,速度为每秒$\frac{π}{6}$个单位长度,则第2015秒时,点P的坐标是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图所示,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发.沿这条曲线向右运动,速度为每秒$\frac{π}{6}$个单位长度,则第2015秒时,点P的坐标是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
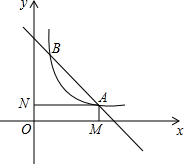 函数y=6-x与函数y=$\frac{4}{x}$交于A、B两点,过点A作x轴与y轴的垂线,垂足分别为M、N,则四边形OMAN的面积和周长分别为多少?
函数y=6-x与函数y=$\frac{4}{x}$交于A、B两点,过点A作x轴与y轴的垂线,垂足分别为M、N,则四边形OMAN的面积和周长分别为多少?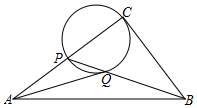 如图,在Rt△ABC中,∠C=90°,AC=4,AB=5,在线段AC上有一动点P(P不与C重合),以PC为直径作⊙O交PB于Q点,连AQ,则AQ的最小值为$\frac{\sqrt{73}-3}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=4,AB=5,在线段AC上有一动点P(P不与C重合),以PC为直径作⊙O交PB于Q点,连AQ,则AQ的最小值为$\frac{\sqrt{73}-3}{2}$.