题目内容
7. 如图所示,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发.沿这条曲线向右运动,速度为每秒$\frac{π}{6}$个单位长度,则第2015秒时,点P的坐标是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图所示,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发.沿这条曲线向右运动,速度为每秒$\frac{π}{6}$个单位长度,则第2015秒时,点P的坐标是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
分析 根据圆的周长即点P运动的速度得出点P的运动周期为12s,由2015÷12═167…11知第2015秒时点P的坐标与第11秒时点P的坐标相同,再根据三角函数的定义求得点P11的坐标,从而得出答案.
解答 解:根据题意知,半圆的周长为π,
点P运动两个半圆所需时间为$\frac{2π}{\frac{π}{6}}$=12(s),
∴点P的运动周期为12s,
∵2015÷12═167…11,
∴第2015秒时点P的坐标与第11秒时点P的坐标相同,
如图,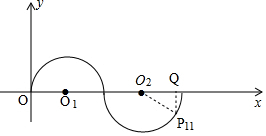
过点P11作P11Q⊥x轴于点Q,
由题意知O2P11=1,∠P11O2Q=30°,
∴O2Q=O2P11sin∠P11O2Q=$\frac{1}{2}$,O2Q=O2P11cos∠P11O2Q=$\frac{\sqrt{3}}{2}$,
则第2015秒时,点P的坐标是(167×4+$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),即($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$),
故答案为:($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
点评 本题主要考查点的坐标变化规律,根据圆的周长即点P运动的速度得出点P的运动周期为12s,从而得出第2015秒时点P的坐标与第11秒时点P的坐标相同是解题的关键.

练习册系列答案
相关题目
17.已知G为△ABC的重心,过G的直线交AB于P,交AC于Q,设$\frac{AP}{PB}$=a,$\frac{AQ}{QC}$=b,则$\frac{1}{a}$+$\frac{1}{b}$=1.
2.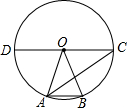 如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )
如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )
 如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )
如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 70° |
14.已知$\frac{a}{b}$=$\frac{1}{3}$,则$\frac{b-a}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
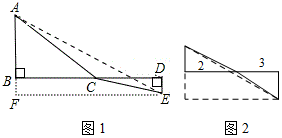 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CE=x
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CE=x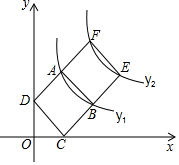 如图,在边长均为1的正方形ABCD和ABEF中,顶点A,B在双曲线y1=$\frac{{k}_{1}}{x}$(k1≠0)上,顶点E,F在双曲线y2=$\frac{{k}_{2}}{x}$(k2≠0)上,顶点C,D分别在x轴和y轴上,则k1=1,k2=3.
如图,在边长均为1的正方形ABCD和ABEF中,顶点A,B在双曲线y1=$\frac{{k}_{1}}{x}$(k1≠0)上,顶点E,F在双曲线y2=$\frac{{k}_{2}}{x}$(k2≠0)上,顶点C,D分别在x轴和y轴上,则k1=1,k2=3.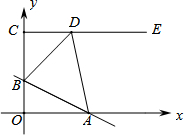 如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.
如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.